Plantilla:Criterios de semejanza de triángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:28 21 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:27 7 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema | + | {{Teorema_sin_demo |
| |titulo=Criterios de semejanza de triángulos | |titulo=Criterios de semejanza de triángulos | ||
| |enunciado= | |enunciado= | ||
| Línea 5: | Línea 5: | ||
| #Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales: <math>\widehat{A}=\widehat{A}',\ \widehat{B}=\widehat{B}'</math> | #Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales: <math>\widehat{A}=\widehat{A}',\ \widehat{B}=\widehat{B}'</math> | ||
| #Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido: <math>\frac {a}{a'} = \frac {b}{b'} \ , \ \widehat{C}=\widehat{C}'</math> | #Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido: <math>\frac {a}{a'} = \frac {b}{b'} \ , \ \widehat{C}=\widehat{C}'</math> | ||
| - | |||
| - | |demo= | ||
| - | # | ||
| - | #En efecto, si tienen dos ángulos respectivamente iguales, el tercero también lo tienen igual. Entonces, esos dos triángulos se pueden poner en la posición de Tales y, en consecuencia, son semejantes. | ||
| - | # | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:27 7 may 2017
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen los lados proporcionales:
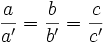
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
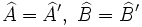
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
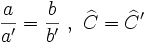
Criterios de semejanza de triángulos Descripción: En esta escena podrás ver los tres criterios de semejanza de triángulos.
