Distancias en el plano (1ºBach)
De Wikipedia
| Revisión de 16:10 21 may 2017 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 16:10 21 may 2017 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) Ir a siguiente diferencia → |
||
| Línea 79: | Línea 79: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Distancias en el plano|enunciado= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Distancia de un punto a una recta | |titulo1=Distancia de un punto a una recta | ||
| Línea 87: | Línea 88: | ||
| *Ejemplos. | *Ejemplos. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejercicio resuelto: ''Distancias en el plano'' | ||
| - | |enunciado=Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5). | ||
| - | |sol= | ||
| - | Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura. | ||
| - | |||
| - | '''Solución:''' Área=10 u<sup>2</sup>. | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | {{Videotutoriales|titulo=Distancias en el plano|enunciado= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 182: | Línea 171: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejercicio resuelto: ''Distancias en el plano'' | ||
| + | |enunciado=Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5). | ||
| + | |sol= | ||
| + | Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura. | ||
| - | ===Ejercicios propuestos=== | + | '''Solución:''' Área=10 u<sup>2</sup>. |
| + | }} | ||
| + | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Distancias en el plano'' | |titulo=Ejercicios propuestos: ''Distancias en el plano'' | ||
Revisión de 16:10 21 may 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 203)
Distancia ente dos puntos
La distancia entre dos puntos 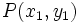 y
y 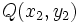 es igual al módulo del vector
es igual al módulo del vector 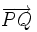 :
:
|
|
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
En esta escena podrás ver como se calcula la distancia entre dos puntos del plano.
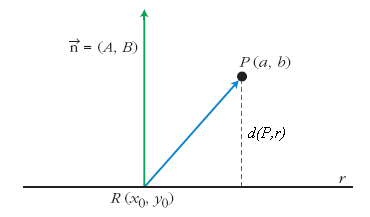
Distancia de un punto a una recta
Proposición
- La distancia del punto
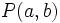 a la recta
a la recta 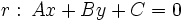 es:
es:
|
|
En esta escena podrás ver como se calcula la distancia de un punto a una recta utilizando vectores, tal y como se ha visto en la demostración anterior.
En esta escena podrás ver como se calcula la distancia de un punto a una recta utilizando una construcción simple, de las que se denominan de "regla y compás".
Ejemplo: Distancia de un punto a una recta
En esta escena vamos a hallar la distancia del punto 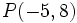 a la recta
a la recta 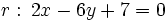 .
.
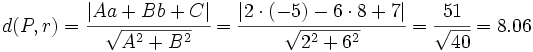
Hazlo tú:
Calcula la distancia del punto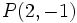 a la recta
a la recta 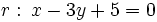 y comprueba el resultado en la escena anterior.
y comprueba el resultado en la escena anterior.- Cálculo de la distancia de un punto a una recta.
- Ejemplos.
Ejercicio sobre el cálculo de la distancia de un punto a una recta (2 métodos)
En este vídeo calculamos la distancia de un punto a una recta identificada en forma continua. Problema típico de examen. No es admisible dejarlo escapar.
En este vídeo calculamos la distancia de un punto a una recta identificada en forma paramétrica. Problema típico de examen. No es admisible dejarlo escapar.
Dos ejercicios sobre distancia de un punto a una recta en los que una de las coordenadas del punto es un parámetro "k" que hay que averiguar conocido el valor de la distancia.
Hay que determinar la recta que pasa por un punto dado y equidista de dos puntos dados. Típico de examen. No puede dejarse escapar.
Hay que determinar el punto de una recta dada "r" cuya distancia a la recta dada "s" es conocida. Típico de examen. No puede dejarse escapar.
Dados dos puntos "P" y "Q", hay que determinar la recta que pasa por "P" y está a distancia dada de "Q". Típico de examen. No es admisible dejarlo escapar.
Dados dos vértices de un triángulo equilatero, debemos determinar el tercer vértice. Típico de examen. No puede dejarse escapar.
Problema típico de examen sobre triángulos uno de cuyos vértices tiene una coordenada desconocida que hay que determinar, conocida el área. No es admisible dejarlo escapar.
La solución que damos sirve para ilustrar el uso de "ventanas", que facilitan la tarea a tu profe y le hacen feliz.
Determinar un punto de una recta que determina con otros dos puntos dados un triángulo de área dada.
Nos dan tres vértices consecutivos de un paralelogramo y debemos determinar el cuarto vértice y el área del paralelogramo. Otro ejemplo de uso de "ventanas"..... esfuérzate en aprender a emplearlas.
Ejercicio resuelto: Distancias en el plano
Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5).
Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura.
Solución: Área=10 u2.Ejercicios propuestos
|
Ejercicios propuestos: Distancias en el plano |
Distancia entre dos rectas
La distancia entre dos rectas paralelas "r" y "s" es la distancia a la recta "s" de un punto cualquiera de la recta "r".
Cálculo de la distancia entre dos rectas paralelas
- La "distancia" entre dos rectas paralelas "r" y "s" es la distancia a la recta "r" de un punto cualquiera de la recta "s".
- Ejemplos.
Determina el área de un cuadrado dos de cuyos lados están situados en sendas rectas dadas.
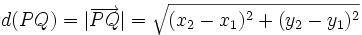
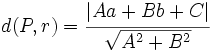
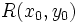 un punto de la recta.
un punto de la recta.
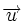
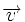
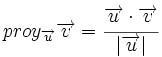
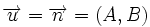
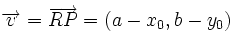
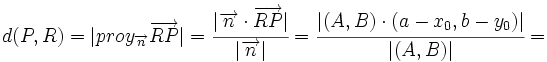
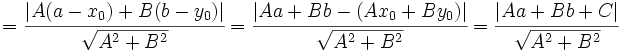
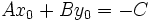 , por ser
, por ser 
