Lenguaje algebraico. Utilidad (1º ESO)
De Wikipedia
| Revisión de 09:49 31 may 2017 Coordinador (Discusión | contribuciones) (→Expresión de números desconocidos y planteamiento de ecuaciones) ← Ir a diferencia anterior |
Revisión de 09:53 31 may 2017 Coordinador (Discusión | contribuciones) (→Uso de letras en lugar de números) Ir a siguiente diferencia → |
||
| Línea 33: | Línea 33: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Vamos a ver algunas situaciones en la que tenemos que recurrir a expresar los números mediante letras. | + | En los siguientes ejemplos vamos a ver algunas situaciones en la que tenemos que recurrir a expresar los números mediante letras: |
| {{p}} | {{p}} | ||
| - | ===Expresión de propiedades o reglas=== | + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= |
| - | Por ejemplo, la '''propiedad conmutativa del producto''' de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera: | + | *'''Expresión de propiedades o reglas''' |
| + | Por ejemplo, la ''propiedad conmutativa del producto'' de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera: | ||
| <center><math>a \cdot b = b \cdot a \;</math></center> | <center><math>a \cdot b = b \cdot a \;</math></center> | ||
| - | La '''regla de la división''' dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera: | + | La ''regla de la división'' dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera: |
| <center><math>D= d \cdot c +r \;</math></center> | <center><math>D= d \cdot c +r \;</math></center> | ||
| - | ===Expresión de fórmulas=== | + | *'''Expresión de fórmulas''' |
| Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras: | Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras: | ||
| Línea 50: | Línea 51: | ||
| {{p}} | {{p}} | ||
| - | ===Generalización de relaciones numéricas=== | + | *'''Generalización de relaciones numéricas''' |
| Si consideramos la siguiente sucesión numérica | Si consideramos la siguiente sucesión numérica | ||
| Línea 58: | Línea 59: | ||
| <center><math>7^2 = 49\;</math></center> | <center><math>7^2 = 49\;</math></center> | ||
| - | ===Expresión de números desconocidos y planteamiento de ecuaciones=== | + | *'''Expresión de números desconocidos y planteamiento de ecuaciones''' |
| Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar | Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar | ||
| Línea 64: | Línea 65: | ||
| donde estamos utilizando la letra <math>x\;</math> para representar al primer número y la expresión <math>x+1\;</math> para representar al segundo número. | donde estamos utilizando la letra <math>x\;</math> para representar al primer número y la expresión <math>x+1\;</math> para representar al segundo número. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Expresiones algebraicas|enunciado= | {{Videotutoriales|titulo=Expresiones algebraicas|enunciado= | ||
Revisión de 09:53 31 may 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 170)
Uso de letras en lugar de números
Las matemáticas muchas veces requieren trabajar con números cuyo valor es desconocido o variable. En tales casos, los números se representan mediante letras y se operan con ellas utilizando las mismas propiedades que cuando trabajamos con números. A esto se le llama traducir al lenguaje algebraico. De su estudio se encarga la parte de las matemáticas denominada álgebra.
Letras en lugar de números. El lenguaje algebraico te permitirá plantear ecuaciones para resolver problemas.
En los siguientes ejemplos vamos a ver algunas situaciones en la que tenemos que recurrir a expresar los números mediante letras:
- Expresión de propiedades o reglas
Por ejemplo, la propiedad conmutativa del producto de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera:
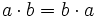
La regla de la división dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera:
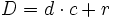
- Expresión de fórmulas
Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras:
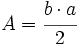
- Generalización de relaciones numéricas
Si consideramos la siguiente sucesión numérica
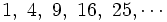
la expresión 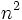 sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra
sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra  por el número 7,
por el número 7,
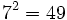
- Expresión de números desconocidos y planteamiento de ecuaciones
Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar
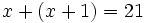
donde estamos utilizando la letra  para representar al primer número y la expresión
para representar al primer número y la expresión 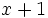 para representar al segundo número.
para representar al segundo número.
Paso de lenguaje habitual a lenguaje algebraico y viceversa.
Como se traducen expresiones del lenguaje cotidiano a expresiones algebraicas y su uso en el planteamiento de ecuaciones.
Como se traducen expresiones del lenguaje cotidiano a expresiones algebraicas y su uso en el planteamiento de ecuaciones.
Ejercicios propuestos
|
Ejercicios propuestos: Uso de letras en vez de números |

