Fórmula del binomio de Newton (1ºBach)
De Wikipedia
| Revisión de 07:38 3 jun 2017 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) ← Ir a diferencia anterior |
Revisión de 11:35 13 jun 2017 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) Ir a siguiente diferencia → |
||
| Línea 95: | Línea 95: | ||
| b) <math>(x-y)^5\;</math> | b) <math>(x-y)^5\;</math> | ||
| |url1=https://www.youtube.com/watch?v=W3idpDs9y4E&list=PL9B9AC3136D2D4C45&index=24 | |url1=https://www.youtube.com/watch?v=W3idpDs9y4E&list=PL9B9AC3136D2D4C45&index=24 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 3 | ||
| + | |duracion=15´23" | ||
| + | |url1=https://www.youtube.com/watch?v=KV2TlE7KdVk&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=53 | ||
| + | |sinopsis=Desarrolla usando el triángulo de Tartaglia: <math>(a+b)^5\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 4 | ||
| + | |duracion=10´08" | ||
| + | |url1=https://www.youtube.com/watch?v=vmv0VIBglc4&index=54&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis= | ||
| + | a) Halla el segundo término del desarrollo por el binomio de Newton de <math>(2x^2+1)^6\;</math> | ||
| + | |||
| + | b) Halla el coeficiente del quinto término del desarrollo por el binomio de Newton de <math>(3a+b)^6\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 5 | ||
| + | |duracion=10´10" | ||
| + | |url1=https://www.youtube.com/watch?v=J90qsLwUEDA&index=55&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis= | ||
| + | a) Halla el término independiente del desarrollo por el binomio de Newton de <math>\left( x^2+\cfrac{1}{x^2}\right)^6\;</math> | ||
| + | |||
| + | b) La diferencia del número de términos de los binomios <math>(a+b)^m\;</math> y <math>(a+b)^n\;</math> es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n". | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 11:35 13 jun 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(pág 45)
Binomio de Newton
Teorema: Fórmula del binomio de Newton El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula:
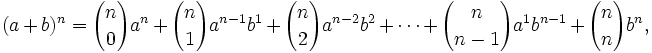
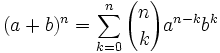 siendo
|
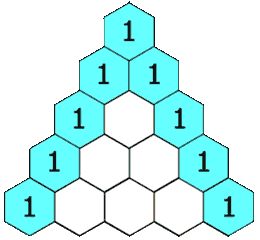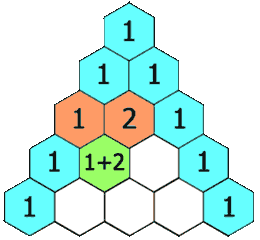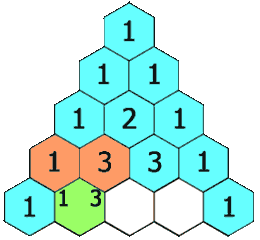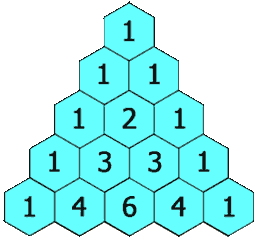
Triángulo de Pascal
|
El triángulo de Pascal es una representación de los coeficientes binomiales ordenados en forma triangular. 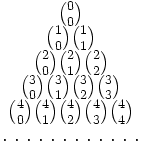 También conocido como triángulo de Tartaglia, especialmente en Italia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77).
Propiedades
Demostración:
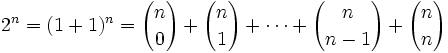
|
Tutorial en el que se explica la construcción del Triángulo de Pascal o Triángulo de Tartaglia y se aplica para el desarrollo de potencias de binomios. También se explica la relación con el Binomio de Newton.
Desarrolla usando el triángulo de Tartaglia y números combinatorios:
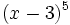
Desarrolla usando el triángulo de Tartaglia y por otro método:
a) 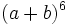
b) 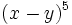
Desarrolla usando el triángulo de Tartaglia: 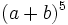
a) Halla el segundo término del desarrollo por el binomio de Newton de 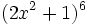
b) Halla el coeficiente del quinto término del desarrollo por el binomio de Newton de 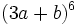
a) Halla el término independiente del desarrollo por el binomio de Newton de 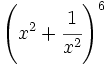
b) La diferencia del número de términos de los binomios 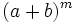 y
y 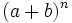 es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n".
es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n".
Ejercicios propuestos
|
Ejercicios propuestos: Binomio de Newton |
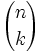 , los
, los 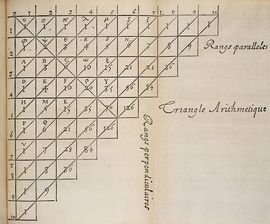
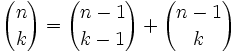 . [1]
. [1]
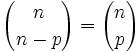 . [2]
. [2]