Plantilla:Multiplicación ángulos
De Wikipedia
| Revisión de 08:21 6 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:54 6 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Para la multiplicación analítica de un ángulo en sexagesimal en forma compleja por un número natural, debemos multiplicar por ese número cada una de las unidades del ángulo (grados, minutos y segundos). Si alguno de los productos de los segundos o minutos es superior a 60, lo transformamos en una unidad de orden inmediatamente superior. Veamos un ejemplo: | + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= |
| + | Para multiplicar analíticamente un ángulo en sexagesimal, en forma compleja, por un número natural: | ||
| + | |||
| + | #Multiplicamos por ese número cada una de las unidades del ángulo (grados, minutos y segundos). | ||
| + | #Si alguno de los productos de los segundos o minutos es superior a 60, lo transformamos en una unidad de orden inmediatamente superior. | ||
| + | }} | ||
| + | |||
| + | Veamos un ejemplo: | ||
| {{Ejemplo | {{Ejemplo | ||
Revisión de 08:54 6 jul 2017
Multiplicar un ángulo por un número natural equivale a sumar el ángulo consigo mismo tantas veces como indique el número.
- La multiplicación gráfica de un ángulo por un número natural se hace colocando el ángulo en posición de consecutivo consigo mismo tantas veces como indique el número.
- La multiplicación analítica se realiza multiplicando el número por la amplitud del ángulo.
Multiplicación de un ángulo por un número Descripción: Actividad en la que podrás ver como se multiplican ángulos por números naturales de forma gráfica y de forma analítica en forma simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Procedimiento
Para multiplicar analíticamente un ángulo en sexagesimal, en forma compleja, por un número natural:
- Multiplicamos por ese número cada una de las unidades del ángulo (grados, minutos y segundos).
- Si alguno de los productos de los segundos o minutos es superior a 60, lo transformamos en una unidad de orden inmediatamente superior.
Veamos un ejemplo:
Ejemplo: Multiplicación de un ángulo por un número
Calcula la siguiente multiplicación de un ángulo en sexagesimal en forma compleja por un número natural:
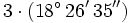
18º 26' 35" x 3 _______________ 54º 78' 105"
Pero 105" = 1' 45", luego
54º 79' 45"
Pero 79' = 1º 19', luego
55º 19' 45"
Multiplicación de un ángulo por un número Descripción: Realiza en tu cuaderno las siguientes multiplicaciones de ángulos en sexagesimal en forma compleja:
- a) 56º 20' 40" x 2
- b) 37º 42' 15" x 4
- c) 125º 15' 30" x 3
Multiplicaciones de ángulos en sexagesimal en forma compleja:
Ejercicio 1 (3'34") Sinopsis: Calcula: (25º 12' 37")· 5
Ejercicio 2 (3'04") Sinopsis: Calcula: (50º 18")· 20
Ejercicio 3 (2'54") Sinopsis: Calcula: (72º 31')· 17
