Simetrías (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:36 17 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:43 17 jul 2017 Coordinador (Discusión | contribuciones) (→Simetría axial) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
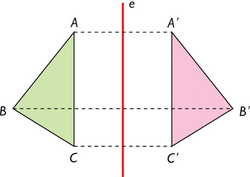
| {{Caja_Amarilla|texto=*Dada una recta "e" y un punto C que no pertenezca a ella, vamos a buscar otro punto C' con la condición de que la recta sea la mediatriz del segmento CC'. El punto C' así buscado se llamará '''simétrico''' de C y la recta "e" se llamará '''eje de simetría'''. Si el punto C perteneciese a la recta, su simétrico sería él mismo. | {{Caja_Amarilla|texto=*Dada una recta "e" y un punto C que no pertenezca a ella, vamos a buscar otro punto C' con la condición de que la recta sea la mediatriz del segmento CC'. El punto C' así buscado se llamará '''simétrico''' de C y la recta "e" se llamará '''eje de simetría'''. Si el punto C perteneciese a la recta, su simétrico sería él mismo. | ||
| {{p}} | {{p}} | ||
| - | *Este tipo de simetría se denomina '''simetría axial''' o '''reflexión''' y se puede aplicar a cualquier figura geométrica. Para ello representamos los simétricos de todos los vértices de la figura original y obtenemos así otra figura simétrica a la primera. | + | *Este tipo de simetría se denomina '''simetría axial''' o '''reflexión''' y se puede aplicar a cualquier figura geométrica. Para ello representamos los simétricos de todos los vértices de la figura original y obtenemos así otra figura simétrica a la primera. |
| - | }} | + | *Una figura plana diremos que es simétrica respecto de un eje, si cualquier punto de la figura tiene su simétrico respecto de dicho eje en la propia figura.}} |
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Dado un punto A, para obtener su simétrico, A', respecto de una recta "e", se siguen los siguientes pasos: | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Dado un punto A, para obtener su simétrico, A', respecto de una recta "e", se siguen los siguientes pasos: | ||
| Línea 20: | Línea 20: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Proposición|enunciado=Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes contiguos forman un ángulo de <math>\cfrac{180^\circ}{n}</math>.}} | ||
| {{Videotutoriales|titulo=Simetría axial o reflexión|enunciado= | {{Videotutoriales|titulo=Simetría axial o reflexión|enunciado= | ||
| {{Video_enlace_carreon|titulo1=Tutorial 1 | {{Video_enlace_carreon|titulo1=Tutorial 1 | ||
| Línea 52: | Línea 54: | ||
| |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/06.htm | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/11/06.htm | ||
| }} | }} | ||
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes contiguos forman un ángulo de <math>\cfrac{180^\circ}{n}</math>.}} | + | |
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 16:43 17 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Simetría axial
 Procedimiento Dado un punto A, para obtener su simétrico, A', respecto de una recta "e", se siguen los siguientes pasos:
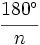Proposición Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes contiguos forman un ángulo de   Tutorial 1 (3'54") Sinopsis: La simetría axial. Ejemplos.  Tutorial 2 (3'54") Sinopsis: En este vídeo trazamos la simetría axial de un polígono.  Simetría axial Descripción:
|  |
.
Actividad: Ejes de simetría Descripción: 
