Parámetros estadísticos

De Wikipedia

(Diferencia entre revisiones)

Revisión de 17:01 20 jun 2007

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Si estamos estudiando la estatura de todos los alumnos y alumnas del instituto y necesitamos dar información de este estudio, parece lógico dar un dato que conocemos todos como media y que representa la estatura de todo el alumnado estudiado. Además de este dato existen otros datos (que llamaremos parámetros) que van a representar a toda la población o que nos van a informar sobre la población.

Parámetros estadísticos. Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:

Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos vamos a estudiar la media aritmética, la moda y la mediana.

Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Por ejemplo el recorrido, la varianza y la desviación típica.

Parámetros de Centralización

Media aritmética

Se define la media aritmética como la suma de todos los datos dividida por el número de datos. Se representa por 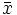$\bar x\$ .

Para calcular la media aritmética hacemos:

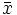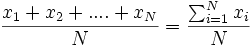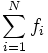
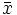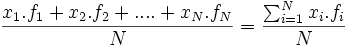
$\bar x\$ = $\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N}$ donde N = nº total de individuos= $\sum_{i=1}^N f_i$ Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula: $\bar x\$ = $\frac{x_1.f_1 + x_2.f_2 + ....+x_N.f_N} {N}={\sum_{i=1}^N x_i.f_i \over N}$ Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como

x i

las marcas de clase: los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.

Actividad Interactiva: Media aritmética

Actividad 1. Variable discreta.

Actividad:

Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividad 2. Variable continua.

Actividad:

Calcula en tu cuaderno el histograma para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tienes en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividad 1:

a) Tanto en un caso como en otro modifica las frecuencias y observa como puede variar el valor de la media.

b) ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.

c) ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.

Actividad 2:

En el caso de la estatura, se ha calculado la media utilizando intervalos, pero como tenemos pocos valores de la variable, calcúlala ahora utilizando la definición, es decir, suma todos las estaturas y divide el resultado por el número de alumnos y alumnas que hay. ¿Coincide el resultado? ¿Por qué ?

Obtenido de "http://maralboran.org/wikipedia/index.php/Par%C3%A1metros_estad%C3%ADsticos"

 </center>
 Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como <math> x_i</math> '''las marcas de clase''': los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.
+{{p}}
+{{AI2|titulo=Actividad Interactiva: ''Media aritmética''|cuerpo=
+{{ai_cuerpo
+|enunciado='''Actividad 1'''. Variable discreta.
+|actividad= Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
+<center><iframe>
+url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/graficos/diagrama_barras_est.htm
+width=100%
+height=600
+name=myframe
+</iframe></center>}}
+{{ai_cuerpo
+|enunciado='''Actividad 2'''. Variable continua.
+|actividad= Calcula en tu cuaderno el histograma para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
+<center><iframe>
+url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/graficos/diagrama_barras_est.htm
+width=100%
+height=600
+name=myframe
+</iframe></center>}}
+}}
+{{p}}
+<div style="background: white; border: 2px solid red; border-left: 4px solid red;border-bottom: 4px solid red; padding:.75em;">
+'''Actividad 1:'''
+a) Tanto en un caso como en otro modifica las frecuencias y observa como puede variar el valor de la media.
+b) ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
+c) ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
+</div>
+{{p}}
+<div style="background: white; border: 2px solid red; border-left: 4px solid red;border-bottom: 4px solid red; padding:.75em;">
+'''Actividad 2:'''
+En el caso de la estatura, se ha calculado la media utilizando intervalos, pero como tenemos pocos valores de la variable, calcúlala ahora utilizando la definición, es decir, suma todos las estaturas y divide el resultado por el número de alumnos y alumnas que hay. ¿Coincide el resultado? ¿Por qué ?
+</div>

Parámetros estadísticos

De Wikipedia

Revisión de 17:01 20 jun 2007

Parámetros de Centralización

Media aritmética

Vistas

Herramientas personales

Menú

Buscar

Herramientas