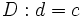Plantilla:Def division

(Diferencia entre revisiones)

Revisión de 13:20 6 ago 2017

La división de D entre d consiste en repartir una cantidad, D, en partes iguales de tamaño d, distinto de 0.
- Se representa por $D : d=c\;$ .
- A D lo llamaremos dividendo, a d divisor y a c cociente.
Hay que distinguir dos casos:
- Si d está contenido en D un número "exacto" de veces (el cociente, c, es un número natural tal que D=d·c), diremos que la división es exacta.
- En caso contrario diremos que la división es entera. Si ocurre esto, es posible encontrar un número natural r, lo más pequeño posible, de manera que si se lo restamos al dividendo, D, y dividimos el resultado por el divisor, d, la división es exacta. A dicho número r, lo llamaremos resto o residuo de la división.

20:4 = 5

 *Hay que distinguir dos casos:
 **Si ''d'' está contenido en  ''D'' un número "exacto" de veces (el cociente, ''c'', es un número natural tal que D=d·c), diremos que la división es '''exacta'''.
-**En caso contrario diremos que '''es entera'''. Si ocurre esto, es posible encontrar un número natural ''r'', lo más pequeño posible, de manera que si se lo restamos al dividendo, ''D'', y dividimos el resultado por el divisor, ''d'', la división es exacta. A dicho número ''r'', lo llamaremos '''resto''' o '''residuo''' de la división.
+**En caso contrario diremos que la división '''es entera'''. Si ocurre esto, es posible encontrar un número natural ''r'', lo más pequeño posible, de manera que si se lo restamos al dividendo, ''D'', y dividimos el resultado por el divisor, ''d'', la división es exacta. A dicho número ''r'', lo llamaremos '''resto''' o '''residuo''' de la división.
 }}
 }}