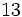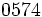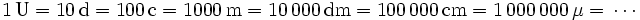Estructura de los números decimales (1º ESO)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 09:42 27 ago 2017

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Los números decimales
2 Representación de los números decimales
- 2.1 Ejercicios propuestos
3 Orden en los números decimales
- 3.1 Ejercicios propuestos
4 Tipos de números decimales
5 Aproximación por redondeo
- 5.1 Ejercicios propuestos

(Pág. 86)

Los números decimales

Los números decimales se utilizan para expresar cantidades comprendidas entre dos números enteros.

Para empezar Descripción:

Los números decimales aparecen si un valor está comprendido entre dos números enteros. En esta actividad podrás medir con una regla virtual la longitud de algunos segmentos.

Los siguientes videos resumen todo lo que vamos a ver en los siguientes apartados y más.

Los números decimales

Tutorial 1 (7'15") Sinopsis:

Introducción a los números decimales. Lectura de números decimales. Uso de los números decimales.

Tutorial 2a (7'39") Sinopsis:

En este video se explica qué son los números decimales y cuáles son sus partes: unidades, décimas, centésimas y milésimas.

Tutorial 2b (10'52") Sinopsis:

En este video se explican las clases de números decimales que existen: limitados e ilimitados. Dentro de los ilimitados encontramos decimales no periódico y periódicos. Y dentro de los decimales periódicos nos encontramos con periódicos puros o mixtos.

Partes de un número decimal

Un número decimal es un número que consta de dos partes separadas por un punto (o coma), llamado punto (o coma) decimal:

Parte entera: Es la parte que indica las unidades completas y, por tanto, corresponde a un número entero. Va delante del punto (o coma) decimal.
Parte decimal: Es la parte que indica las unidades menores que la unidad y, por tanto, corresponde a un número comprendido entre 0 y 1. Va detrás del punto (o coma) decimal.

Observación:

Actualmente, en la lengua española se emplean básicamente tres formas de anotar un número con parte decimal, según el signo empleado como separador decimal:

El punto decimal: se emplea un punto (.) para separar la parte entera de la decimal, este método es el utilizado en las calculadoras electrónicas y en los ordenadores, rara vez se utiliza en la notación de cifras manualmente.

3.141592

La coma decimal: se emplea una coma (,) como separador, esta forma en común en las publicaciones de habla hispana y se utiliza también en las notaciones manuales.

3,141592

El apóstrofo decimal: el apóstrofo (') en ocasiones también llamado coma decimal es la forma usual de separar la parte decimal de un número en las notaciones a mano.

3′141592

En todos los casos, las cifras decimales, no se separan en grupos con espacios en blanco u otro signo, sino que se escriben seguidas, sea cual sea el número de cifras decimales que forme la parte decimal del número en cuestión.

En cuanto al uso por países, unos utilizan preferentemente la coma decimal, mientras que otros, como los alglosajones, utilizan el punto decimal. Si quieres más información puedes consultar e siguiente enlace:

Separador decimal

Ejemplo

El número $13.0574 \;$ tiene:

Parte entera: $13\;$
Parte decimal: $0574\;$

Partes de un número decimal

Tutorial 1 (1'00") Sinopsis:

Los números decimales. Partes de un número decimal.

Tutorial 2 (1'00") Sinopsis:

Los números decimales. Partes de un número decimal. Utilidad de los números decimales.

Órdenes de unidades decimales

Los órdenes de unidades decimales se utilizan para expresar números menores que la unidad y tienen la misma estructura que los de la parte entera:

Una unidad de cualquier orden se divide en diez unidades del orden inmediato inferior. Según su posición a la izquierda de la coma o punto decimal, tenemos por orden:

La décima (d), que es el resultado de dividir la unidad en diez partes iguales.
La centésima (c), que es el resultado de dividir una décima en diez partes iguales o una unidad en cien partes iguales.
La milésima (m), que es el resultado de dividir una centésima en diez partes iguales o una unidad en mil partes iguales.
La diezmilésima (dm), que es el resultado de dividir una milésima en diez partes iguales o una unidad en diez mil partes iguales.
La cienmilésima (cm), que es el resultado de dividir una diezmilésima en diez partes iguales o una unidad en cien mil partes iguales.
La millonésima (mm ó $μ$ ), que es el resultado de dividir una cienmilésima en diez partes iguales o una unidad en un millón de partes iguales.

etc.

$1 \, \mbox{U} = 10 \, \mbox{d} = 100 \, \mbox{c} = 1000 \, \mbox{m} = 10\,000 \, \mbox{dm} = 100\,000 \, \mbox{cm} =1\,000\,000 \, \mu =\, \cdots\;$

Órdenes de unidades decimales

Actividad 1 Descripción:

Actividad en la que aprenderás mediante ejemplos los órdenes de unidades decimales.
Actividad para comprobar lo aprendido en la actividad anterior.

Actividad 2 Descripción:

Valor posicional decimal.

Autoevaluación 1a Descripción:

Elige el número decimal representado en la imagen.

Autoevaluación 1b Descripción:

Escribe el número decimal representado en la imagen.

Órdenes de unidades decimales

Tutorial (7'26") Sinopsis:

0:00-3:12: Los número decimales. Para qué sirven.
3:12-7:26: Relación de los decimales con las fracciones. (se verá en un tema posterior)

Ejercicio 1 (3'31") Sinopsis:

a) ¿Cuántas décimas son 20 centésimas?

b) ¿Cuántas centésimas son 8 décimas?

c) ¿Cuántas unidades son 600 centésimas?

d) ¿Cuántas centésimas son 3 unidades?

e) ¿Cuántas milésimas hay en 5 centésimas?

f) ¿Cuántas milésimas hay en 6 décimas?

Ejercicio 2 (7'37") Sinopsis:

1) Transforma en euros:

a) 85 céntimos

b) 3 euros y 8 céntimos

c) 5 céntimos

d) 105 céntimos

e) 1 euro 25 céntimos

f) 280 céntimos

2) Expresa en céntimos:

a) 0.08 €

b) 1.5 €

c) 0.15 €

d) 1.08 €

e) 0.20 €

f) 2.35 €

Lectura y escritura de los números decimales

Para leer un número decimal:

Se nombra la parte entera expresada en unidades.
Se nombra la parte decimal expresada en el orden de unidades de la cifra decimal que queda a la derecha.

Ejemplo

El número:

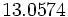
$13.0574 \;$

Se lee:

"Trece unidades y quinientas setenta y cuatro diezmilésimas"

Las cifras ocupan los siguientes órdenes de unidades:

C	D	U.	d	c	m	dm	cm	mm
	1	3.	0	5	7	4
	1 decena	3 unidades	0 decimas	5 centésimas	7 milésimas	4 diezmilésimas

Lectura y escritura de números decimales

Tutorial 1 (4'21") Sinopsis:

Partes de un número decimal. Lectura de números decimales.

Tutorial 2 (5'23") Sinopsis:

Lectura y escritura de números decimales.

Ejercicio 1 (2'02") Sinopsis:

Lee y descompón los siguientes números decimales en sus distintos órdenes: 1.150, 6.12, 8.025

Ejercicio 2 (3'58") Sinopsis:

Escribe con cifras:

a) Cinco unidades y tres décimas.

b) Ocho unidades y cinco décimas.

c) Doce unidades y dos décimas.

d) Ocho unidades y veinticinco centésimas.

e) Trece unidades y cincuenta centésimas.

f) Doce unidades y cinco centésimas.

g) Cinco milésimas.

h) Doscientas cuarenta milésimas.

i) Tres unidades y cinco milésimas.

j) Doce unidades y ochenta y dos milésimas.

Ejercicio 3 (4'39") Sinopsis:

1) Escribe con cifras:

1a) 3U+5d+4c+2m

1b) 4U+1c+5m

1c) 8U+8m

1d) 2U+7d+3m

1e) 12U+4c+3m

2) Escribe como se leen:

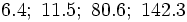
$6.4; \ 11.5; \ 80.6; \ 142.3$

Ejercicio 4 (4'51") Sinopsis:

Escribe números decimales a partir de un gráfico.

Lectura y escritura de números decimales

Actividad Descripción:

Lectura y escritura de números decimales.

Autoevaluación 1 Descripción:

Decimales en forma escrita.

Autoevaluación 2 Descripción:

Escribe decimales dados por gráficos.

Autoevaluación 3 Descripción:

En las frases siguientes, identificad el valor del número descrito. Si no acertáseis a la primera, podréis intentarlo de nuevo, pero perderéis puntos.

Representación de los números decimales

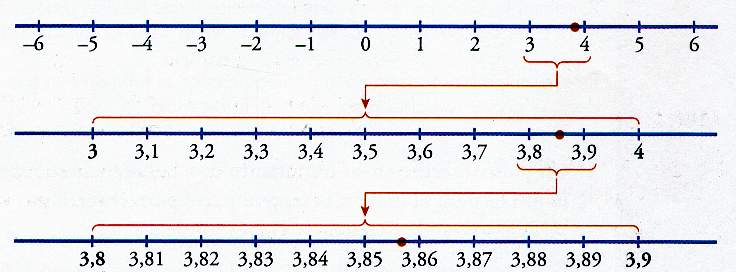
Los números decimales los podemos representar en la numérica real de la siguiente manera:

Para representar las décimas dividimos la unidad en 10 partes.
Para representar las centésimas dividimos cada décima en 10 partes.
Para representar las milésimas dividimos cada centésima en 10 partes, y así continuaríamos para las diez milésimas, cien milésimas, etc.

El punto rojo representa el número 3,85...

Representación gráfica de los números decimales

Tutorial 1 (2'22") Sinopsis:

Representación gráfica de los números decimales en la recta numérica.

Tutorial 2 (1'52") Sinopsis:

Representación gráfica de los números decimales en la recta numérica.

Tutorial 3 (10'35") Sinopsis:

Representación gráfica de los números decimales en la recta numérica.

Tutorial 4 (1'27") Sinopsis:

Representación gráfica de los números decimales en la recta numérica.

Ejercicio 1 (1'21") Sinopsis:

Representa 0.6 en la recta numérica.

Ejercicio 2 (2'12") Sinopsis:

Identifica números decimales en la recta numérica.

Ejercicio 3 (1'21") Sinopsis:

Representa en la recta numérica: 3.39, 9.04, 5.93

Ejercicio 4 (2'59") Sinopsis:

Representa 0.04 en la recta numérica.

Ejercicio 5 (3'34") Sinopsis:

Identifica números decimales en la recta numérica.

Representación gráfica de los números decimales

Actividad Descripción:

Actividad en la que aprenderás a representar números decimales en la recta real.
Actividad para comprobar lo aprendido en la actividad anterior.

Autoevaluación 1 Descripción:

Actividad en la que deberás representar números decimales en la recta real.

Autoevaluación 2 Descripción:

Actividad en la que deberás representar números decimales en la recta real.

Autoevaluación 3a Descripción:

Representación de números decimales con una cifra decimal: Selecciona un número entre -10 y 10 o bien entre -200 y 200 pulsando en el botón correspondiente.

Si el número no se encuentra en la pantalla, mueve el eje hasta encontrarlo y posteriormente arrastra la bola hasta la posición buscada.

Autoevaluación 3b Descripción:

Representación de números decimales con dos o tres cifras decimales:

Selecciona una de las dos opciones, o un número decimal con dos cifras decimales o un decimal con tres cifras decimales pulsando en el botón correspondiente.

Si el número no se encuentra en la pantalla, mueve el eje hasta encontrarlo y posteriormente arrastra la bola hasta la posición buscada.

Autoevaluación 3c Descripción:

Decimal comprendido entre dos:

Debes de colocar un número decimal comprendido entre los dos decimales que ofrece la pantalla.

Autoevaluación 4a Descripción:

Identifica decimales en la recta numérica (décimas).

Autoevaluación 4b Descripción:

Identifica decimales en la recta numérica (centésimas).

Ejercicios propuestos

Ejercicios propuestos: Estructura de los números decimales

(Pág. 87)

1; 2a,b,f; 3a,b; 4a,e,i; 5; 7; 8

2c,d,e; 4b,c,d,f,g,h; 6

Orden en los números decimales

Procedimiento: Ordenación de números decimales

Dados dos números decimales:

Si tienen partes enteras diferentes, es mayor el que tiene mayor parte entera.
Si tienen la misma parte entera, localizamos la primera posición decimal en la que tengan cifras diferentes, empezando a comprobar desde la coma hacia la derecha.
- Si son positivos, es mayor el que tiene la mayor de esas dos cifras.
- Si son negativos, es mayor el que tiene la menor de esas dos cifras.

Truco

Para realizar el procedimiento anterior resulta útil colocar los números a comparar uno encima del otro, haciendo coincidir la coma o punto decimal. Puedes verlo en el siguiente ejemplo.

Ejemplo:

1. Compara y ordena los siguientes números: 3.25 y 3.4

Solución:

Colocamos las cifras una encima de la otra, haciendo coincidir la coma decimal:

 3.25
 3.40

Como las partes enteras son iguales (3), comparamos las partes decimales:

Como 4 > 2, y el número es positivo, el segundo número es mayor.

Por tanto, 3.4 > 3.25

2. Compara y ordena los siguientes números: -3.225 y -3.231

Solución:

Colocamos las cifras una encima de la otra, haciendo coincidir la coma decimal:

 -3.225
 -3.231

Como las partes enteras son iguales (-3), comparamos las partes decimales:

Las cifras de las décimas son iguales (2), luego comparo la de las centésimas.

Como 3 > 2, y el número es negativo, el primer número es mayor.

Por tanto, -3.225 > -3.231

Orden en los números decimales

Tutorial 1 (0'41") Sinopsis:

Comparación de números decimales. Ejemplos.

Tutorial 2 (6'27") Sinopsis:

Comparación de números decimales. Ejemplos.

Tutorial 3 (4'09") Sinopsis:

Comparación de números decimales. Ejemplos.

Tutorial 4 (9'36") Sinopsis:

Ejemplos de comparación de números decimales. Ejercicios propuestos y resueltos.

Ejercicio 1 (1'39") Sinopsis:

Compara 45.675 y 45.645.

Ejercicio 2 (3'28") Sinopsis:

Compara 156.378 y 156.348.

Ejercicio 3 (3'28") Sinopsis:

Ordena de menor a mayor: 0.0790, 0.0709, 0.07, 0.0097 y 0.7090.

Ejercicio 4 (1'29") Sinopsis:

Ordena de menor a mayor: 0.5610, 0.605, 0.165, 0.52 y 0.151.

Ejercicio 5 (3'19") Sinopsis:

Ordena de mayor a menor: 0.35, 0.035, 0.305 y 3.50

Orden en los números decimales

Actividad Descripción:

Actividad en la que aprenderás mediante ejemplos a ordenar números decimales.

Autoevaluación 1a Descripción:

Actividad para practicar la comparación de dos números decimales.

Autoevaluación 1b Descripción:

Actividad para practicar la ordenación de varios números decimales.

Autoevaluación 2a Descripción:

Comparar decimales (décimas y centésimas).

Autoevaluación 2b Descripción:

Comparar decimales hasta las milésimas.

Autoevaluación 2c Descripción:

Compara valor posicional decimal.

Autoevaluación 2d Descripción:

Ordena decimales.

Autoevaluación 3 Descripción:

Ejercicios de autoevaluación sobre el orden en los números decimales.

Proposición

Los números decimales "completan" la recta numérica, es decir, para cada punto de la recta hay un número decimal y para cada decimal hay un punto de la recta.
Entre dos números decimales distintos siempre hay infinitos números decimales.

Ejemplo:

Considera los números 2.3 y 2.4.

a) Encuentra números decimales comprendidos ellos.

b) Averigua uno que esté a la misma distancia de ambos.

Solución:

a) Escribimos nuestros decimales con una cifra más, añadiendo un cero: 2.30 y 2.40.

Buscamos números comprendidos entre 30 y 40:

31, 32, 33, ... , 38, 39

y los colocamos en la parte decimal:

2.30 < 2.31 < 2.32 < 2.33 < 2.34 < 2.35 < 2.36 < 2.37 < 2.38 < 2.39 < 2.40

b) 2.35

Ejercicios propuestos

Ejercicios propuestos: Orden en los números decimales

(Pág. 88)

10, 12

9, 11, 13

Tipos de números decimales

Decimal exacto: Si tiene un número finito de decimales (a partir de una determinada posición, todas los siguientes, hacia la derecha, son cero).
Decimal periódico: Si tiene un número infinito de decimales que se repiten de forma periódica (la misma secuencia una y otra vez indefinidamente).
- Decimal periódico puro: La parte decimal se repite infinitamente y recibe el nombre de período.
- Decimal periódico mixto: Su parte decimal está compuesta por una parte no periódica (anteperiodo) y una parte periódica (período).
No exactos y no periódicos: Si tiene un número infinito de decimales, pero ningún conjunto de esas cifras se repite de forma periódica. A estos números los llamaremos números irracionales.

Notación:

Cuando haya parte decimal periódica, ésta se marcará con el símbolo $\widehat{~} \;$ encima de los números que la formen. Mira los ejemplos que vienen a continuación.

Ejemplos:

Decimal exacto: $2.15\;$

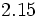
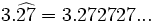
Decimal periódico puro: $3.\widehat{27} =3.272727...$

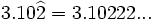
Decimal periódico mixto: $3.10\widehat{2} =3.10222...$

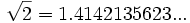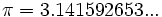
Ilimitados no periódicos: $\sqrt{2} = 1.4142135623...$ ; $\pi=3.141592653...\;$

Clasificación de los números decimales

Tutorial 1 (3'58") Sinopsis:

Clasificación de los números decimales: exactos, periódicos y no periódicos.

Tutorial 2 (6'46") Sinopsis:

Clasificación de los números decimales: exactos, periódicos y no periódicos.

Tutorial 3 (6'21") Sinopsis:

Un enfoque divertido para ver la clasificación de los números decimales: exactos, periódicos y no periódicos.

Ejercicio (13'38") Sinopsis:

Clasifica los siguientes números decimales en limitados (exactos) e ilimitados (periódicos puros o mixtos):

a) 0.5

b) 0.3333...

c) 0.131131131131...

d) 4.8

e) -1.342424242...

f) 0.102030405060...

g) 1.36363636...

h) 0.54

i) 2.33333...

j) 0.1333333...

k) 2.399999...

l) 0.000004

Tipos de números decimales

Actividad Descripción:

Actividad para que puedas aprender a reconocer los tipos de expresiones decimales.

Autoevaluación Descripción:

Ejercicios de autoevaluación sobre tipos de números decimales.

Aproximación por redondeo

Cuando un número tiene muchas cifras, es difícil recordarlo y operar con él. Por eso lo solemos sustituir por otro más manejable de valor similar, prescindiendo de sus últimas cifras. Ese otro número más sencillo decimos que es una aproximación del número de partida.

Procedimiento

Para aproximar un número por redondeo un determinado orden de unidades debemos:

Suprimir todas las cifras a la derecha de dicho orden.
Si la primera cifra suprimida es mayor o igual que cinco se suma una unidad a la cifra anterior. Si no lo es, se deja igual.

Ejercicio resuelto: Aproximación por redondeo

Usa la calculadora y aproxima el resultado, por redondeo, a los gramos.

a) 3 cajas de galletas pesan 4 kg. ¿Cuánto pesa una caja?.

b) 3 cajas de galletas pesan 5 kg. ¿Cuánto pesa una caja?.

Solución:

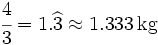
a) $\cfrac{4}{3} = 1.\widehat{3} \approx 1.333 \, \mbox{kg}$

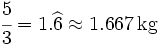
b) $\cfrac{5}{3} = 1.\widehat{6} \approx 1.667 \, \mbox{kg}$

Redondeo de números decimales

Tutorial 1 (8'32") Sinopsis:

Redondeo de números decimales. Ejemplos.

Tutorial 2 (13'17") Sinopsis:

Redondeo de números decimales. Ejemplos y ejercicios propuestos y resueltos.

Tutorial 3 (5'05") Sinopsis:

Redondeo y aproximación de enteros y decimales.

Ejercicio 1 (3'49") Sinopsis:

María está realizando el cálculo del gasto semanal del supermercado. Los tickets tienen los siguientes valores: $74.30, $37.89 y $46.80. Estima el total del gasto redondeando a las decenas.

Aproximación por redondeo

Actividad 1 Descripción:

Actividad para practicar la aproximación por redondeo y truncamiento.

Actividad 2 Descripción:

Actividad para practicar la aproximación por redondeo.

Actividad 3 Descripción:

En esta escena podrás practicar a redondear y truncar números decimales.

Autoevaluación 1 Descripción:

Redondea a las décimas.

Autoevaluación 2 Descripción:

Redondea decimales dados en una recta numérica.

Autoevaluación 3 Descripción:

Redondea decimales.

Autoevaluación 4 Descripción:

Ejercicios de autoevaluación sobre redondeo de números decimales.

Autoevaluación 5 Descripción:

Ejercicios de autoevaluación sobre redondeo de números decimales.

Ejercicios propuestos

Ejercicios propuestos: Aproximación por redondeo

(Pág. 89)

14a,b,c; 15a,b,c

14d,e,f; 15d,e,f

Obtenido de "http://maralboran.org/wikipedia/index.php/Estructura_de_los_n%C3%BAmeros_decimales_%281%C2%BA_ESO%29"

Categorías: Matemáticas | Números

 ==Aproximación por redondeo==
-{{Caja_Amarilla|texto=
+{{Aproximación por redondeo 1ºESO}}
-Cuando un número tiene muchas cifras, es difícil recordarlo y operar con él. Por eso lo solemos sustituir por otro más manejable de valor similar, prescindiendo de sus últimas cifras. Ese otro número más sencillo decimos que es una '''aproximación''' del número de partida.
-}}
-{{p}}
-{{Teorema_sin_demo|titulo=Procedimiento|enunciado=
-Para aproximar un número por '''redondeo'''  un determinado orden de unidades debemos:
-*Suprimir todas las cifras a la derecha de dicho orden.
-*Si la primera cifra suprimida es mayor o igual que cinco se suma una unidad a la cifra anterior. Si no lo es, se deja igual.
-}}
-{{p}}
-{{Ejemplo
-|titulo=Ejercicio resuelto: ''Aproximación por redondeo''
-|enunciado=Usa la calculadora y aproxima el resultado, por redondeo, a los gramos.
-:a) 3 cajas de galletas pesan 4 kg. ¿Cuánto pesa una caja?.
-:b) 3 cajas  de galletas pesan 5 kg. ¿Cuánto pesa una caja?.
-|sol=
-a) <math>\cfrac{4}{3} = 1.\widehat{3} \approx 1.333 \, \mbox{kg}</math>
-b) <math>\cfrac{5}{3} = 1.\widehat{6} \approx 1.667 \, \mbox{kg}</math>
-}}
-{{p}}
-{{AI_cidead
-|titulo1=Aproximación por redondeo
-|descripcion=Actividad para practicar la aproximación por redondo mediante ejercicios resueltos.
-|url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena4/1q4_ejercicios_resueltos_1b.htm
-}}
-{{p}}
-{{Geogebra_enlace
-|descripcion=En esta escena podrás practicar a redondear y truncar números decimales.
-|enlace=[https://ggbm.at/Jk9KdCT5 Redondeo y truncado de números decimales]
-}}
-{{p}}
-{{Video_enlace
-|titulo1=Aproximación por redondeo
-|duracion=5'05"
-|sinopsis=Redondeo y aproximación de enteros y decimales.
-|url1=https://www.youtube.com/watch?v=_Mj5s2dj5h0&list=PLkGU8edrdzbanv7OGbrAqJ0tLVNPTUiz_&index=8
-}}
-{{AI_vitutor
-|titulo1=Autoevaluación: ''Redondeo de números decimales''
-|descripcion=Ejercicios de autoevaluación sobre redondeo de números decimales.
-|url1=http://www.vitutor.com/di/d/a_1e.html
-}}
 ===Ejercicios propuestos===

Estructura de los números decimales (1º ESO)

De Wikipedia

Revisión de 09:42 27 ago 2017

Tabla de contenidos

Los números decimales

Partes de un número decimal

Órdenes de unidades decimales

Lectura y escritura de los números decimales

Representación de los números decimales

Ejercicios propuestos

Orden en los números decimales

Ejercicios propuestos

Tipos de números decimales

Aproximación por redondeo

Ejercicios propuestos

Vistas

Herramientas personales

Menú

Buscar

Herramientas