Funciones lineales (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 22:45 14 oct 2017 Coordinador (Discusión | contribuciones) (→Función lineal) ← Ir a diferencia anterior |
Revisión de 22:48 14 oct 2017 Coordinador (Discusión | contribuciones) (→Función lineal) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| |sinopsis=Representación gráfica de funciones lineales. | |sinopsis=Representación gráfica de funciones lineales. | ||
| }} | }} | ||
| - | {{AI_cidead | + | {{AI_enlace |
| |titulo1=Ejercicio | |titulo1=Ejercicio | ||
| |descripcion=Ejemplo de función lineal. | |descripcion=Ejemplo de función lineal. | ||
| |url1=https://scratch.mit.edu/projects/109762868/#fullscreen | |url1=https://scratch.mit.edu/projects/109762868/#fullscreen | ||
| }} | }} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación: ''Función lineal'' | ||
| + | |descripcion=Ejemplo de función lineal. | ||
| + | |url1=http://www.vitutor.com/fun/1/a_7_e.html | ||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión de 22:48 14 oct 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Función de proporcionalidad
Una función de proporcionalidad directa es aquella cuya expresión analítica puede expresarse como:
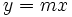 |
 es la variable independiente.
es la variable independiente.
 es la variable dependiente.
es la variable dependiente.
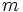 una constante que se denomina constante de proporcionalidad o pendiente.
una constante que se denomina constante de proporcionalidad o pendiente.
En esta escena podrás ver e interactuar con las gráficas de funciones de proporcionalidad directa y estudiar sus propiedades.
Ejemplo de función de proporcionalidad directa.
Ejemplo de función de proporcionalidad directa.
Función lineal
Una función lineal es aquella cuya expresión analítica puede expresarse como:
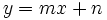 |
 es la variable independiente.
es la variable independiente.
 es la variable dependiente.
es la variable dependiente.
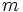 es una constante que se denomina pendiente.
es una constante que se denomina pendiente.
 es otra constante denominada ordenada en el origen. (Si
es otra constante denominada ordenada en el origen. (Si 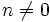 recibe el nombre de función afín)
recibe el nombre de función afín)
En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades.
Ejemplo de función lineal.
Representación gráfica de funciones lineales.
Ejemplo de función lineal.
Ejemplo de función lineal.

