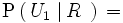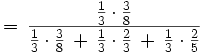Probabilidad. Combinatoria
De Wikipedia
| Revisión de 16:57 29 jun 2007 Juanmf (Discusión | contribuciones) (→Ejemplo) ← Ir a diferencia anterior |
Revisión de 17:02 29 jun 2007 Juanmf (Discusión | contribuciones) (→Ejemplo) Ir a siguiente diferencia → |
||
| Línea 828: | Línea 828: | ||
| \cdot \mathrm{P} | \cdot \mathrm{P} | ||
| \left( | \left( | ||
| - | \, R \, \left| \, U_1 \, \right. | + | \, R \, \left| \, U_1 \, \right) |
| - | \right) | + | |
| } | } | ||
| { | { | ||
Revisión de 17:02 29 jun 2007
Tabla de contenidos |
Experimentos aleatorios
Los fenómenos o experimentos aleatorios son los que pueden dar lugar a varios resultados, sin que pueda ser previsible enunciar con certeza cuál de estos va a ser observado en la realización del experimento.
Espacio muestral
Espacio muestral es el conjunto formado por todos los resultados de un experimento o fenómeno aleatorio. Lo denotamos con la letra E .
Ejemplo: Espacio muestral
El espacio muestral asociado al lanzamiento de dos dados y anotar la suma de los puntos
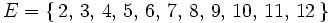
Sucesos
Suceso de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral E . Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas.
Al conjunto de todos los sucesos que ocurren en un experimento aleatorio se le llama espacio de sucesos y se designa por S .
Ejemplo: Sucesos
En el ejemplo anterior, determina los sucesos de E:
a)Salir múltiplo de 5. b)Salir número primo. c)Salir mayor o igual que 10.
a)Salir múltiplo de 5:
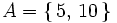
b)Salir número primo:
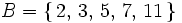
c)Salir mayor o igual que 10:
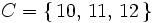
Analicemos los tipos mas frecuentes de sucesos.
Sucesos elementales son los que están formados por un solo resultado del
experimento.
Sucesos compuestos son los que estan formados por dos o más resultados del
experimento; es decir, por dos o más sucesos elementales.
Suceso seguro es el que se verifica al realizar el experimento aleatorio. Está
formado por todos los resultados posibles del experimento y, por tanto, coincide con el
espacio muestral.
Suceso imposible es el que nunca se verifica. Se representa por
.
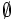Operaciones con sucesos
Inclusión e igualdad de sucesos
Un suceso
A
esta incluido ( contenido ) en otro suceso
B
si todo suceso elemental de
A
pertenece también a
B
. Se representa por
.
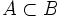Dos suceso A y B son iguales si están formados por los mismos sucesos elementales. Se representa por A = B .
Unión de sucesos
Si tenemos dos sucesos
A
y
B
de un mismo experimento aleatorio, llamamos suceso unión de
A
y
B
al suceso que se realiza cuando lo hacen
A
o
B
. Se representa por
.
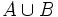Intersección de sucesos
Si tenemos dos sucesos
A
y
B
de un mismo experimento aleatorio, llamamos suceso intersección de
A
y
B
al suceso que se realiza cuando lo hacen
A
y
B
. Se representa por
.
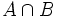Cuando
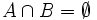, decimos que los sucesos
A
y
B
son incompatibles. Cuando no sucede esto, decimos que
A
y
B
son compatibles.
Sucesos contrarios
Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos conjuntos da el conjunto imposible, decimos que ambos sucesos son complementarios o contrarios.
Para un suceso cualquiera
A
de un experimento aleatorio, llamamos suceso contrario del suceso
A
al suceso que se verifica cuando no se verifica
A
, y reciprocamente. Se representa:
.
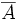En cualquier experimento aleatorio, todo suceso que se considere tiene su contrario. Las
propiedades mas significativas de los sucesos contrarios son:
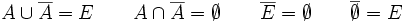
Algebra de Boole de sucesos
La union y la interseccion de sucesos verifican las propiedades conmutativa, asociativa,
idempotente, simplificación, distributiva, existencia de elemento neutro y absorción:
Definición de probabilidad. Propiedades.
Probabilidad condicionada
Llamamos probabilidad condicionada del suceso
B
respecto del suceso
A
, y lo denotamos por
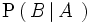al cociente
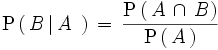
Ejemplo
Se lanzan dos dados. Si la suma ha sido 7, ¿cuál es la probabilidad de que alguno de los dados haya salido un tres?
Sean los sucesos
A = "la suma de los puntos es siete" y
B = "en alguno de los dados ha salido un tres"
El suceso
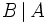es salir en algún dado 3, si la suma ha sido 7. Observamos que esta situación
ocurre en las parejas
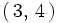y
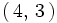. Por tanto,
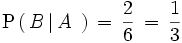
Ejercicios Resueltos
Independencia de sucesos
Decimos que dos sucesos A y B son independientes entre sí si la ocurrencia de uno de ellos no modifica la probabilidad del otro, es decir, si:
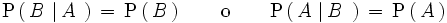
o lo que es lo mismo:
Ejemplos
Calcula la probabilidad de que al extraer 3 cartas, con reemplazamiento, de una baraja española,
sean todas copas.
Como la carta extraída se vuelve a introducir, los sucesos son independientes y la probabilidad buscada es:
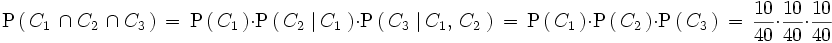
donde Ci denota el suceso salir copas en la extracción número i.
Calcula la probabilidad de que al extraer 3 cartas, sucesivamente, de una baraja española, sean todas copas.
En este caso, los sucesos
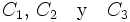no son independientes.
Ejercicios Resueltos
Probabilidad de aprobar cuando sólo se domina parte de la asignatura
Probabilidad de meter un gol en una tanda de penaltis
Probabilidad de obtener dos números pares lanzando dos dados
Teorema de Bayes
Sean
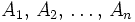sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea
B
un suceso cualquiera del que se conocen las probabilidades condicionales
.
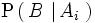Entonces las probabilidades
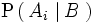vienen dadas por la expresión:
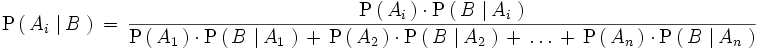
Demostración
Por definición de probabilidad condicionada
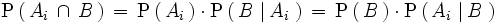
despejando
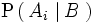, se tiene:
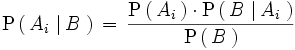
La probabilidad
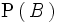, por el teorema de la probabilidad total, es igual a
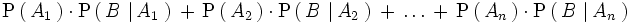
Sustituyendo en la ecuación anterior, obtenemos la fórmula de Bayes.
Ejemplo
Tenemos tres urnas: U1 con tres bolas rojas y cinco negras, U2 con dos bolas rojas y una negra y U3 con dos bolas rojas y tres negras. Escogemos una urna al azar y extraemos una bola. Si la bola ha sido roja, ¿cuál es la probabilidad de haber sido extraída de la urna U1 ?
Llamamos
R
al suceso sacar bola roja. La probabilidad pedida es
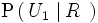. Utilizando el teorema de Bayes, tenemos:
