Las funciones y sus gráficas (3ºESO Académicas)
De Wikipedia
| Revisión de 12:51 25 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:55 25 dic 2017 Coordinador (Discusión | contribuciones) (→Funciones dadas mediante tablas) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| ==Formas de expresar una función== | ==Formas de expresar una función== | ||
| {{Formas de expresar una función}} | {{Formas de expresar una función}} | ||
| + | {{p}} | ||
| + | ===Funciones dadas mediante enunciados=== | ||
| + | {{Funciones dadas mediante enunciados}} | ||
| {{p}} | {{p}} | ||
| ===Funciones dadas mediante tablas=== | ===Funciones dadas mediante tablas=== | ||
| {{Representación de funciones mediante tablas}} | {{Representación de funciones mediante tablas}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Funciones dadas mediante gráficas=== | ===Funciones dadas mediante gráficas=== | ||
| {{Representación gráfica de una función}} | {{Representación gráfica de una función}} | ||
Revisión de 12:55 25 dic 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Actividad de introducción al tema de funciones.
(Pág. 146)
Concepto de función
- Una función es una relación entre dos variables (por ejemplo,
 e
e  ) que a cada valor de
) que a cada valor de  le asigna un único valor de
le asigna un único valor de  .
.
- La variable
 se llama variable independiente y la variable
se llama variable independiente y la variable  se llama variable dependiente, porque su valor depende de
se llama variable dependiente, porque su valor depende de  .
.
- Se dice que
 es función de
es función de  y lo representamos por
y lo representamos por 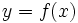 . También se dice que
. También se dice que  es la imagen de
es la imagen de  mediante la función
mediante la función  .
.
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
La relación entre el tiempo (t) que el grifo está abierto y el volumen (V) de agua que hay en el depósito es una función.
El volumen es función del tiempo: 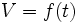
- La variable independiente (t) es el "tiempo que está abierto el grifo".
- La variable dependiente (V) es el "volumen de agua que se ha llenado el depósito".
En los siguientes videos se explican los conceptos básicos sobre funciones que trataremos a lo largo de este tema.
Tutorial en el que se explican los conceptos básicos sobre funciones: variable independiente, dependiente, imagen, preimagen, dominio, recorrido... necesarios para poder comprender la terminología que se emplea en el análisis matemático.
- Definición de función.
- Dominio e imagen (o rango).
- Distintas formas de representar una función.
- Ejercicios resueltos.
Formas de expresar una función
Una función se puede expresar de varias formas:
- Mediante un enunciado que explique la relación que existe entre las variables.
- Mediante una expresión analítica, esto es, una ecuación que relacione las variables.
- Mediante una tabla que contenga los valores de las variables, emparejados.
- Mediante una gráfica, representada en unos ejes cartesianos con una escala adecuada. Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
 , y sobre el eje vertical (eje de ordenadas) la variable dependiente
, y sobre el eje vertical (eje de ordenadas) la variable dependiente  . Cada punto de la gráfica es generado por una pareja de valores
. Cada punto de la gráfica es generado por una pareja de valores  e
e  , que son sus coordenadas
, que son sus coordenadas 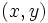 , su abcisa y su ordenada.
, su abcisa y su ordenada.
Consideremos el ejemplo anterior del grifo y el depósito:
1. Enunciado:
- "Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
2. Expresión analítica:
- t = "Tiempo que está abierto el grifo" (en segundos).
- V = "Volumen de agua que se ha llenado el depósito" (en litros).
3. Tabla de valores:
Tiempo (s) |
0 | 1 | 5 | 20 | 40 | 60 | 100 |
Volumen (l) |
0 | 2 | 10 | 40 | 80 | 120 | 200 |
4. Gráfica:
- Representaremos los valores de la tabla en unos ejes de coordenadas. Cada punto de la gráfica consta de dos coordenadas: la primera es el valor de t y la segunda, el valor de V.
|
Actividad: Tabla de valores y gráfica de una función dada por una expresión analítica En el ejemplo anterior hemos trabajado con la función V=2t:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Funciones dadas mediante enunciados
Arjun abrió una cuenta de ahorros el pasado año y puso una cantidad inicial e ella. Sea M(t) el saldo de la cuenta (medido en pesos), a los t días desde que fue abierta. ¿Qué significa la expresión M(30) - M(0) = 100 ?
Sea P(t) el número de personas en la playa de Copacabana en Río de Janeiro, t horas después de la medianoche de un cierto día. ¿Qué significa la expresión P(5) < P(9) ?
Autoevaluación.
Funciones dadas mediante tablas
Tutorial en el que se explican los conceptos básicos de la función y su trabajo en forma de tabla: variable independiente, dependiente, imagen, preimagen, dominio, recorrido...
Nota: Algunos conceptos tratados en este tutorial se verán, más adelante, a lo largo de este tema.
Actividad en la que aprenderás el concepto de función con distintos ejemplos y su representación mediante tabla de valores.
Funciones dadas mediante gráficas
La representación gráfica de una función nos permite visualizar el comportamiento de las dos variables.
Procedimiento
- Usaremos un sistema de ejes cartesianos con una escala adecuada.
- Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
 .
.
- Sobre el eje vertical (eje de ordenadas) la variable dependiente
 .
.
- Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
- Cada punto de la gráfica es generado por una pareja de valores
 e
e  , que son sus coordenadas
, que son sus coordenadas 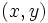 , su abscisa y su ordenada.
, su abscisa y su ordenada.
Consideremos el ejemplo anterior del grifo y el depósito:
- "Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
Función:
El volumen del depósito es función del tiempo: 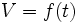
- t = "Tiempo que está abierto el grifo" (en segundos).
- V = "Volumen de agua que se ha llenado el depósito" (en litros).
Tabla de valores:
Para obtener la representación gráfica es necesario obtener puntos de la misma. Para ello construiremos la llamada tabla de valores, que consiste en averiguar parejas de valores (t,V) que estén relacionadas mediante la función:
tiempo (s) |
0 | 1 | 5 | 20 | 40 | 60 | 100 |
Volumen (l) |
0 | 2 | 10 | 40 | 80 | 120 | 200 |
Gráfica:
- Representaremos los valores de la tabla en unos ejes de coordenadas. Cada punto de la gráfica consta de dos coordenadas: la primera es el valor de t y la segunda, el valor de V.
Actividad en la que aprenderás a representar gráficamente una función a partir de su tabla de valores. Las funciones son las que sirvieron de ejemplo en la actividad del apartado anterior.
En esta escena podrás ver como se representan los puntos de la gráfica de una función en unos ejes de coordenadas cartesianos.
La primera parte del tutorial recuerda los conceptos básicos sobre funciones: variable independiente, dependiente, imagen, preimagen, dominio, recorrido... En la segunda parte se muestran ejemplos de funciones dadas mediante gráficas.
Ejemplo de cómo se pueden usar las gráficas de forma engañosa en publicidad.
Las gráficas de contenido matemático se han convertido en el lenguaje más universal de finales del siglo XX. En cualquier medio de comunicación cada vez que se quiere dar información cuantitativa de un proceso aparece una gráfica matemática. Sus ventajas son incuestionables, son capaces de ofrecer gran cantidad de información de un simple vistazo. Constituyen un instrumento imprescindible en campos tan dispares como la medicina, la economía, la física, la biología y hasta en el deporte. En este programa investigaremos su origen relativamente reciente, tienen poco más de 200 años de existencia, y sus distintas aplicaciones y daremos algunos consejos para interpretar de forma crítica la información presentada en forma de gráficas.
Halla f(6) a partir de la gráfica de f(x).
Halla 2·f(8) + 8·g(8) a partir de las gráficas de f(x) y g(x).
Función que relaciona el tiempo que lleva abierto un grifo y la altura que alcanza el nivel del agua en un depósito cilíndrico.
La siguiente escena representa una botella (en color rojo) que cuando abras el grifo se comenzará a llenar de agua. El proceso de llenado de la botella se puede describir matemáticamente con lo que llamamos función, así para un tiempo concreto la función nos dice la altura de la botella en ese momento. El dibujo que queda tras el punto A se llama gráfica de la función.
Haz clic en el botón y dejándolo pulsado observa cómo se llena la botella .
Observa que en el eje horizontal representamos el tiempo que dejamos el grifo abierto y en el vertical la altura que el agua alcanza en la botella. En el eje horizontal hemos empezado a marcar 1 segundo, 2 segundos, etc.
Observa en este ejemplo, que la altura es cero cuando el tiempo transcurrido es cero y que la gráfica va creciendo.
- a) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas.
Si haces clic sobre un punto con el cursor te aparecerán los valores horizontal (tiempo) y vertical (altura) para ese punto.
- b) ¿Qué puedes decir de la relación entre las variables tiempo y altura?
- c) ¿Cuánto tiempo necesita la botella para llenarse hasta la mitad?
- d) ¿Cuánto tiempo necesita la botella para llenarse un cuarto? ¿Y tres cuartos?
Función que relaciona el tiempo que lleva abierto un grifo y la altura que alcanza el nivel del agua en un depósito de forma cónica.
En la siguiente escena la forma de la botella ha cambiado.
- a) Intenta hacer la gráfica antes de ver como queda en la escena.
- b) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas.
- c) ¿Qué puedes decir de la relación entre las alturas y los tiempos?
- d) Ahora la altura del agua según pasa el tiempo sube más despacio, ¿por qué?
Ahora prueba a cambiar la forma de la botella moviendo el punto P.
- e) Haz una botella con la boca más estrecha que la base y observa las distintas gráficas que se generan. Da una explicación de lo qué ocurre.
- f) Las gráficas unas veces son convexas (tipo U) y otras cóncavas (tipo U invertida), ¿de qué depende?
Evalúa funciones a partir de su gráfica.
Evalúa expresiones con funciones.
Reconocer relaciones funcionales a partir de una gráfica.
¿Una recta vertical representa una función?
Reconocer funciones a partir de una tabla.
El valor de y siempre es "tres más que el doble de x". ¿Es y una función de x?
Gaby está comprando regalos en línea. El costo del envío se basa en la cantidad de dinero del pedido. Para pedidos superiores a $20, el coste del envío es $4. Para pedidos de $20 o menos, el coste es del envío es $7. ¿Podemos expresar la cantidad de dinero del pedido en función del coste del envío?
Actividades con las que aprenderás a distinguir relaciones que son función de las que no.
Determina si son o no son funciones las siguientes gráficas.
Una función es una relación entre dos variables numéricas, habitualmente las denominamos  (variable independiente) e
(variable independiente) e  (variable dependiente). Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente.
(variable dependiente). Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente.
Pero además, para que una relación sea función, a cada valor de la variable independiente le debe corresponder un sólo valor de la variable dependiente.
- a) Observa en la escena las gráficas y di cuál de ellas es función y por qué no lo es la otra. Para ello, mueve el punto P y fíjate cuántos puntos de corte tiene la recta azul con cada gráfica. Si es más de uno no es una función.
En esta escena podrás ver, mediante ejemplos gráficos, como algunas relaciones entre variables son función y otras no.
Reconocer relaciones funcionales a partir de gráficas
Reconocer relaciones funcionales a partir de tablas
Dominio e imagen de una función
- El conjunto de valores de la variable independiente,
 , para los que hay un valor de la variable dependiente,
, para los que hay un valor de la variable dependiente,  , se llama dominio de definición de la función. Se denota
, se llama dominio de definición de la función. Se denota 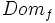 .
.
- El conjunto de valores que toma la variable independiente,
 , se llama imagen, recorrido o rango de la función. Se denota
, se llama imagen, recorrido o rango de la función. Se denota 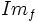 .
.
- Si un punto (x,y) pertenece a la gráfica de la función entonces se dice que y es la imagen de x y también que x es la antiimagen de y.
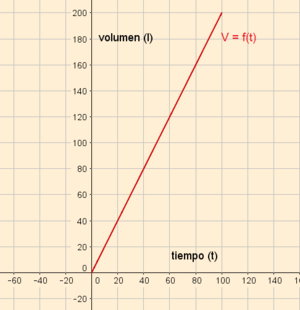
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
- t = "Tiempo que está abierto el grifo".
- V = "Volumen de agua que se ha llenado el depósito".
- Dominio: El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos:
![Dom_f=[0,100]\;](/wikipedia/images/math/a/b/d/abd624243bc89fe5a2233724f02b4f4a.png)
- Recorrido: El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros:
![Im_f=[0,200]\;](/wikipedia/images/math/3/9/f/39fa0225481adedcbe46a7b134738d1a.png)
Tutorial en el que se explica el cálculo del dominio y la imagen de una función a partir de su gráfica.
Halla el dominio de una función a partir de su gráfica:
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Halla la imagen de una función a partir de su gráfica:
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Halla el dominio de una función a partir de un enunciado:
Pati tiene una hermosa planta. La planta empezó a retoñar 2 días antes de que Pati la comprara, y la tuvo por 98 días antes de que muriera. La altura máxima que alcanzó a planta fue de 30 cm. Si denotamos por h(t) la altura de la planta en cm tras transcurrir t días desde el día de la compra, indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Thomas tiene 400 barras de caramelo en su tienda, y cada una cuesta $0.50. Sea p(b) el precio, medido en pesos ($), de la compra de b barras de caramelo. Indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Mason está parado en el 5º escalón de una escalera vertical. La escalera tiene 15 escalones y la diferencia de altura entre escalones consecutivos es de 0.5 m. Él está pensando si sube, baja o se queda quieto. Sea h(n) la altura por encima del nivel del suelo de los pies de Mason (medido en metros) después de moverse n escalones (si Mason bajara n escalones , n es negativa). Indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Imagen y antiimagen:
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Dada la gráfica de la función g(x), halla la antiimagen de -2, es decir, el valor de x para el cual g(x) = -2.
Dada la gráfica de la función f(x), halla el valor de x, además de -5, para el cual f(x) = f(-5).
Dada la función f(t) = -2t + 5, halla la antiimagen de 13, es decir, el valor de t para el cual f(t) = 13.
Actividades en las que aprenderás de forma visual los conceptos de dominio y recorrido de una función.
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X, ¿Cuál es su dominio y su imagen?
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
¿Cuál es su dominio y su imagen?
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
¿Cuál es su dominio y su imagen?
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
Dominio y rango a partir de gráficas.
Dominio de una función dada por un enunciado.
Imagen y antiimagen:
Actividades con las que aprenderás los conceptos de imagen y antiimagen.
Halla la antiimagen utilizando la gráfica de la función.
Halla la antiimagen utilizando la expresión analítica de la función.
Puntos de corte con los ejes de una función
Los puntos de corte con los ejes de una función son los puntos de la gráfica que pertenecen a los ejes de coordenadas:
- Puntos de corte con el eje de abscisas (eje X): Son aquellos puntos de la función en los que la variable dependiente,
 , toma el valor cero.
, toma el valor cero.
- Punto de corte con el eje de ordenadas (eje Y): Es aquel punto de la función en el que la variable independiente,
 , toma el valor cero.
, toma el valor cero.
Tutorial en el que se explica el cálculo de los puntos de corte con los ejes de una función dada su gráfica.
Estudio de los puntos de corte con los ejes de una función a partir de su gráfica.
Estudio de los puntos de corte con los ejes de una función a partir de su gráfica.
Estudio de los puntos de corte con los ejes de una función a partir de su gráfica.
Estudio de los puntos de corte con los ejes de una función a partir de su gráfica.
Actividades con las que aprenderás a calcular los puntos de corte con los ejes de una función.
Signo de una función
- Una función decimos que es positiva cuando la variable dependiente toma valores positivos y decimos que es negativa cuando toma valores negativos.
- El estudio del signo de una función consistirá en determinar para qué valores de la variable independiente la función es positiva o negativa.
Tutorial en el que se explica el estudio del signo de una función dada su gráfica.
Existe un error en el minuto 5:05 cuando se expresa los valores donde se alcanzan valores positivos, ya que el valor máximo que puede tomar la x es 6 y no infinito
Estudio del signo de una función a partir de su gráfica.
Estudio del signo de una función a partir de su gráfica.
Estudio del signo de una función a partir de su gráfica.
Estudio del signo de una función a partir de su gráfica.
Actividad en la que debes averiguar los intervalos donde la función es positiva o negativa.
Variables discretas y continuas
En una función, la variable independiente puede ser:
- Continua: Si toma valores en intervalos. En consecuencia, siempre toma infinitos valores. La gráfica de la función estará formada por trazos.
- Discreta: Si los valores que toma la variable están separados (no toma valores en ningún intervalo). Puede tomar un número finito o infinito de valores. La gráfica de la función estará formada por puntos separados.
- Son variables continuas: El peso de una persona, la velocidad de un móvil, la altura de un triángulo, etc. De forma más general, una variable que tome valores en el conjunto de los números reales, en un intervalo real o en la unión de varios intervalos reales.
- Son variables discretas: El número de hijos de una familia, el número de trabajadores de una plantilla, el número de alumnos de un curso, etc. De forma más general, una variable que tome valores en el conjunto de los números enteros o en un subconjunto suyo.
En la papelería de la esquina compramos bolígrafos a 0.30 €, cada uno. Relaciona el número de bolígrafos comprados y el precio de la compra.
Tabla de valores:
a) Completa la tabla:
bolígrafos |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
precio |
Gráfica:
Para representar gráficamente una función utilizamos unos ejes cartesianos con una escala adecuada. En el eje horizontal representamos el número de bolígrafos que compramos. En el eje vertical representamos el precio de la compra. Para cada valor que le asignes al número de bolígrafos se marca en su vertical el precio de esos bolígrafos con un punto rojo.
En la parte inferior de la escena asígnale a la variable bolígrafos los valores de la tabla anterior y observa su precio, es decir, la altura donde se coloca el punto rojo.
b) ¿Cuáles son las escalas utilizadas en la gráfica?, es decir: ¿qué mide un cuadradito cualquiera del eje horizontal? y ¿qué mide un cuadradito cualquiera del eje vertical?
c) Fijándote en la gráfica, ¿cuánto cuestan 16 bolígrafos?. ¿Cuántos bolígrafos te dan por 3,60 €?
d) ¿Tiene sentido unir los puntos rojos de la gráfica? ¿Por qué?
e) ¿Cuál es el dominio y el recorrido de esta función?
Vamos al mercado a comprar patatas. El precio de 1 kg es de 0.30 €. Relaciona el número de kilos de patatas adquiridos y su coste.
El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas.
Pero hay una importante diferencia entre ambos ejemplos: no podemos comprar fracciones de bolígrafos (1.5 o 2.7 bolígrafos) y en cambio sí podemos comprar fracciones de kilos de patatas (1.5 o 2.7 kilos de patatas).
Tabla de valores:
a) Calcula y anota los precios de las siguientes cantidades de patatas. Asígnale esos valores a la variable kilos de la escena siguiente.
kilos de patatas |
0 | 1 | 1,5 | 2 | 2,7 | 5 | 5,7 | 7 |
precio |
Gráfica:
b) ¿Tiene sentido ahora unir los puntos rojos de la gráfica?
Compuébalo en la escena asignándole a la variable kilos el valor 0 y a continuación, mantén pulsado el botón del ratón sobre la fecha superior de los kilos de patatas.
En el primer caso, la gráfica estaba formada por puntos aislados. En este segundo caso, la gráfica es una línea continua.
c) ¿Cuál es el dominio y el recorrido de esta función?
Actividades y videotutoriales
Plantilla:Actividades y videos: Evaluar funciones
|
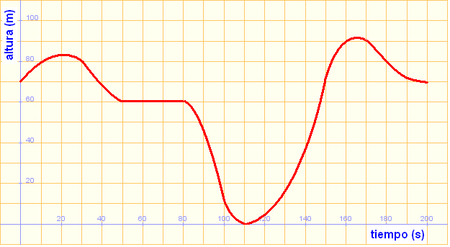
Ejercicios resueltos: Interpretación de gráficas La siguiente gráfica describe el vuelo de un águila desde que sale del nido hasta que vuelve a él con una presa que caza durante el trayecto.
Solución:
|
|
Ejercicio resuelto: Dominio e imagen |
Ejercicios propuestos
|
Ejercicios propuestos: Las funciones y sus gráficas |


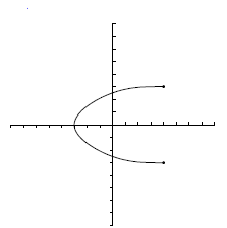
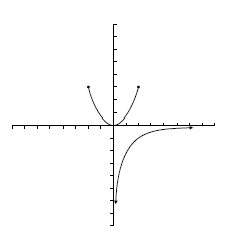
![Dom=[-3.5, 4]\;\!](/wikipedia/images/math/c/b/4/cb4d06ad9717b5428bfec1aa7001daab.png) .
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
.

