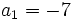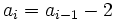Plantilla:Término general de una progresión aritmética
De Wikipedia
| Revisión de 11:36 27 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:09 27 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 71: | Línea 71: | ||
| ---- | ---- | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicios | + | |titulo1=Ejercicio 1 |
| + | |duracion=6´39" | ||
| + | |url1=https://youtu.be/_6WrqWRbcxI | ||
| + | |sinopsis= | ||
| + | #Una progresión aritmética tiene como término general <math>a_i=4+3(i-1)\;</math>, halla el término <math>a_{20}\;</math>. | ||
| + | #Halla el término <math>a_5\;</math> de una progresión aritmética que viene dada por la siguiente ley de recurrencia: | ||
| + | ::<math>a_1=-7\;</math> | ||
| + | ::<math>a_i=a_{i-1}-2\;</math> | ||
| + | |||
| + | |||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 2 | ||
| |duracion=7´08" | |duracion=7´08" | ||
| |url1=https://youtu.be/RaXRADJxsTI | |url1=https://youtu.be/RaXRADJxsTI | ||
| Línea 82: | Línea 94: | ||
| }} | }} | ||
| {{Actividades|titulo=Término general de una progresión aritmética|enunciado= | {{Actividades|titulo=Término general de una progresión aritmética|enunciado= | ||
| - | {{AI_cidead | + | {{AI_Khan |
| |titulo1=Actividad 1 | |titulo1=Actividad 1 | ||
| + | |descripcion=Actividad de introducción a las fórmulas de sucesiones aritméticas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/sequences/introduction-to-arithmetic-squences/a/using-formulas-of-arithmetic-sequences | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 2 | ||
| |descripcion=Actividades en las que aprenderás a obtener el término general de una progresión aritmética. | |descripcion=Actividades en las que aprenderás a obtener el término general de una progresión aritmética. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena5/3quincena5_contenidos_2b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena5/3quincena5_contenidos_2b.htm | ||
| Línea 89: | Línea 106: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Encuentra el término general de una progresión aritmética dada. | |descripcion=Encuentra el término general de una progresión aritmética dada. | ||
| - | |enlace=[http://ggbm.at/fuNJJNQd Actividad 2] | + | |enlace=[http://ggbm.at/fuNJJNQd Actividad 3] |
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación | ||
| + | |descripcion=Usa fórmulas de sucesiones aritméticas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/sequences/introduction-to-arithmetic-squences/e/arithmetic_sequences_2 | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 12:09 27 dic 2017
Término general de una progresión aritmética
El término general, 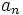 , de una progresión aritmética de diferencia
, de una progresión aritmética de diferencia  es:
es:
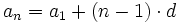
En efecto, de forma intuitiva:
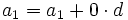
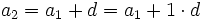
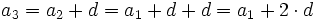
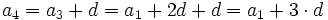
........................
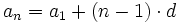
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
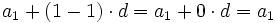
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
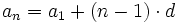 . [1]
. [1]Por ser una progresión aritmética cada término se obtiene sumando d al anterior término:
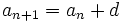 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n+ d \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 + (n-1) \cdot d + d =a_1 + ((n+1)-1) \cdot d](/wikipedia/images/math/7/4/4/744cf81c67660fb80f54db415de019dd.png)
- Definición de progresión aritmética.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones aritméticas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
- Definición de progresión aritmética.
- Ejemplos
- Término general
- Una progresión aritmética tiene como término general
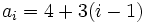 , halla el término
, halla el término 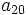 .
.
- Halla el término
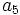 de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Halla el término general y la forma recursiva de las siguientes progresiones aritméticas:
- a) {-5, -3, -1, 1, ...}
- b) {100, 107, 114, 121, ...}
- c) {1, 3, 6, 10, ...}
Actividad de introducción a las fórmulas de sucesiones aritméticas.
Actividades en las que aprenderás a obtener el término general de una progresión aritmética.
Encuentra el término general de una progresión aritmética dada.
Usa fórmulas de sucesiones aritméticas.