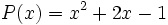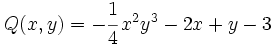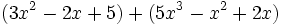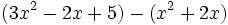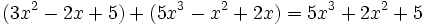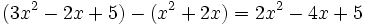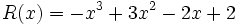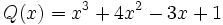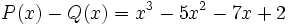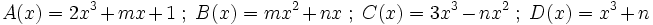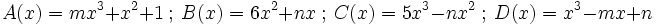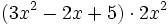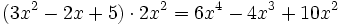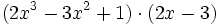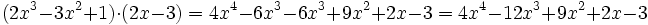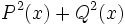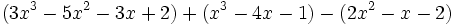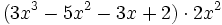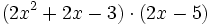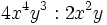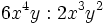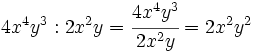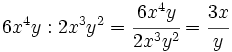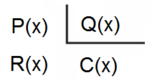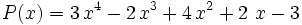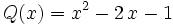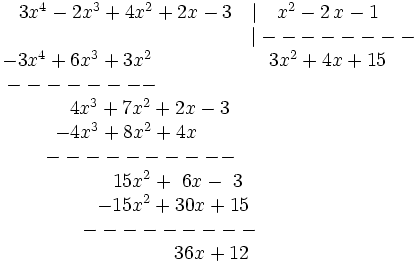Polinomios. Operaciones (4ºESO Académicas)
De Wikipedia
| Revisión de 17:16 15 sep 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:19 15 sep 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| {{p}} | {{p}} | ||
| ==Operaciones con polinomios== | ==Operaciones con polinomios== | ||
| - | {{operaciones con polinomios}} | + | ===Suma y resta de polinomios=== |
| + | {{Suma y resta de polinomios}} | ||
| {{p}} | {{p}} | ||
| + | ===Producto de un monomio por un polinomio=== | ||
| + | {{producto monomio polinomio}} | ||
| + | {{p}} | ||
| + | ===Producto de polinomios=== | ||
| + | {{Producto de polinomios}} | ||
| + | {{p}} | ||
| + | |||
| + | {{p}} | ||
| + | ===División de monomios=== | ||
| + | {{division de monomios}} | ||
| + | {{p}} | ||
| + | ===División de un polinomio entre un monomio=== | ||
| + | {{División de un polinomio entre un monomio}} | ||
| + | {{p}} | ||
| + | |||
| ===División de polinomios=== | ===División de polinomios=== | ||
| {{división de polinomios}} | {{división de polinomios}} | ||
| + | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 17:19 15 sep 2018
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Calculadora |
Tabla de contenidos |
Polinomios
|
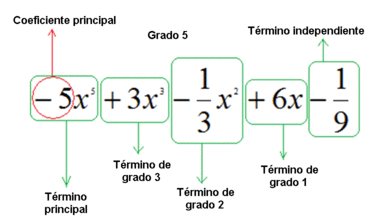
Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis.
Por ejemplo:
a) El polinomio 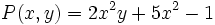 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
b) El polinomio 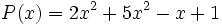 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 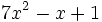 . Es de grado 2.
. Es de grado 2.
c) Los polinomios constantes, como por ejemplo 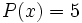 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 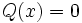 , tiene grado cero.
, tiene grado cero.
d) Los polinomios 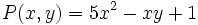 y
y 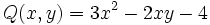 son semejantes.
son semejantes.
e) Los polinomios 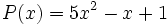 y
y 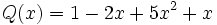 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes...
Polinomios. Grado de un polinomio. Ejemplos.
Polinomios. Grado de un polinomio. Ejemplos.
Aprende a calcular el grado relativo y absoluto de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
- Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos.
- Valor numérico de un polinomio.
Polinomios. Monomios. Grado y término independiente de un polinomio.
1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
- a)
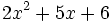
- b)
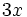
- c)
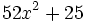
- d)
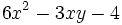
- e)
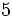
- f)
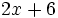
2) Expresa en forma reducida los siguientes polinomios:
- a)
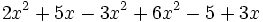
- b)
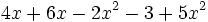
- c)
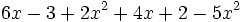
- d)
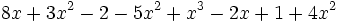
3) Indica el grado de cada polinomio:
- a)
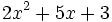 ; b)
; b) 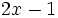 ; c)
; c) 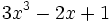
- d)
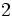 ; e)
; e) 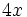 ; f)
; f) 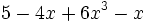
- g)
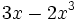 ; h)
; h) 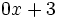 ; i)
; i) 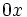
4) Indica cuáles de estos polinomios son iguales:
- a)
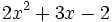 ; b)
; b) 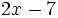 ; c)
; c) 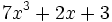 ; d)
; d) 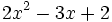
- e)
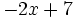 ; f)
; f) 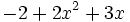 ; g)
; g) 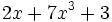 ; h)
; h) 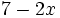
- i)
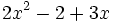 ; j)
; j) 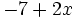 ; k)
; k) 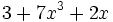 ; l)
; l) 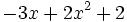
5) Indica cuáles de estos polinomios son semejantes entre sí:
- a)
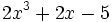 ; b)
; b) 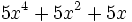 ; c)
; c) 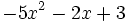
- d)
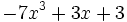 ; e)
; e) 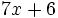 ; f)
; f) 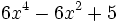
- g)
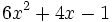 ; h)
; h) 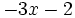
6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
- a)
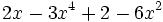
- b)
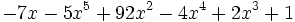
- c)
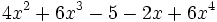
- d)
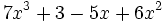
- e)
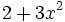
- f)
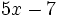
7) Clasificar polinomios en homogéneos/heterogéneos.
- a)
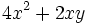
- b)
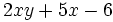
- c)
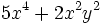
- d)
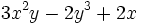
- e)
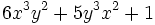
- f)
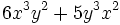
- g) 5x3 − 6y3
Dado el polinomio 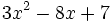 , identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
Escribe un polinomio que exprese el valor de "p" billetes de 20 pesos, "q" monedas de 10 pesos y "r" monedas de 5 pesos.
Elementos y grado de un polinomio.
Expresiones algebraicas: monomios y polinomios.
- Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación.
- Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos.
- Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio.
- Actividad en la que aprenderás a escribir polinomios en su forma usual.
- Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio.
Actividad sobre polinomios.
Operaciones con polinomios
Suma y resta de polinomios
Procedimiento
Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.
Aprende a sumar y restar polinomios
En este tutorial se explica la suma y resta de polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.
Aprende a sumar polinomios
Aprende a restar polinomios
Suma y resta de polinomios en una variable. Ejemplos.
Suma de polinomios. Ejemplos.
Propiedades de la suma de polinomios: conmutativa y asociativa.
Propiedades de la suma de polinomios: Elemento neutro y opuesto.
Resta de polinomios. Equivalencias fundamentales.
Suma y resta de polinomios.
Calcula la suma: 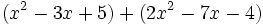
Calcula la suma: 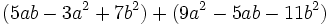
Calcula la resta: 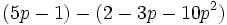
Calcula la resta: 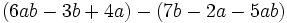
Calcula:
a) 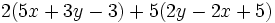 b)
b) 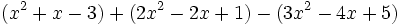
Simplifica: 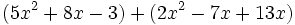
Simplifica: 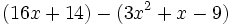
Resta 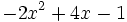 de
de 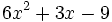 .
.
Simplifica: 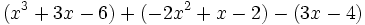
Simplifica: 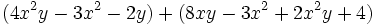
Simplifica: 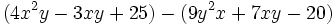
Resta 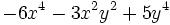 de
de 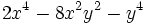 .
.
Encuentra el error cometido en la resta que se muestra en el video.
1) Ordena los polinomios y realiza las sumas que se indican:
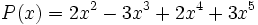 ;
; 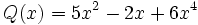
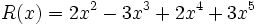 ;
; 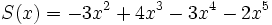
1a) P(x) + Q(x)
1b) P(x) + R(x)
1c) P(x) + S(x)
Dados los siguientes polinomios, realiza las sumas que se indican:
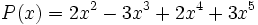 ;
; 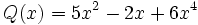
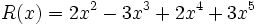 ;
; 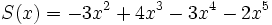
1d) Q(x) + S(x)
1e) R(x) + S(x)
1f) Q(x) + R(x)
2) Sumas los siguientes polinomios y compara el grado del polinomio suma con el grado de los polinomios sumandos.
3a) Escribe opuestos de los siguientes polinomios:
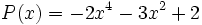 ;
; 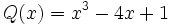
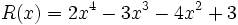 ;
; 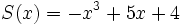
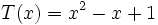 ;
; 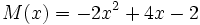
3b) Suma cada uno de los polinomios del apartado anterior con su opuesto.
3c) Calcula un polinomio A(x) tal que 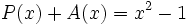 , siendo
, siendo 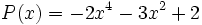 .
.
Dados los siguientes polinomios:
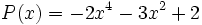 ;
; 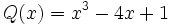
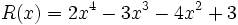 ;
; 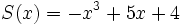
3d) Calcula un polinomio B(x) tal que 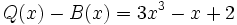 .
.
3e) Calcula un polinomio C(x) tal que 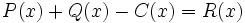 .
.
3f) Calcula un polinomio D(x) tal que 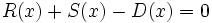 .
.
Dados los polinomios:
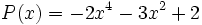 ;
; 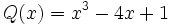
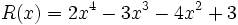 ;
; 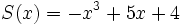
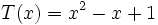 ;
; 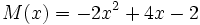
4a) Calcula P(x) - Q(x).
4b) Calcula P(x) - R(x).
4c) Calcula [P(x) + Q(x)]-[R(x) + S(x)]
4d) Calcula [P(x) + S(x)]-[Q(x) + R(x)]
4e) Calcula T(x) + M(x)
4f) Calcula T(x) - M(x)
5) ¿Qué polinomio se ha de restar al polinomio 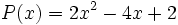 para obtener el polinomio
para obtener el polinomio 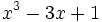 ?
?
6) Dados los polinomios
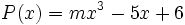 ;
; 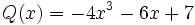
calcula el valor de  sabiendo que
sabiendo que 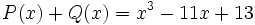 .
.
7) Escribe dos polinomios de tercer grado de tal modo que su suma se el polinomio nulo.
8) Escribe dos polinomios reducidos de segundo grado y comprueba con ellos la conmutatividad de la suma.
9) Dado el polinomio 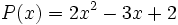 , escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.
, escribe su opuesto, -P(x). Calcula los valores numéricos de P(x) y -P(x) para x = 0, x = 1 y x = 2, y comprueba comprueba que son números opuestos.
10) ¿Qué polinomio tienes que sumar con 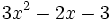 para que la suma sea 5x^3-6x?
para que la suma sea 5x^3-6x?
11) Dado el polinomio 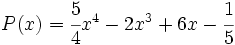 , halla otro polinomio Q(x) tal que
, halla otro polinomio Q(x) tal que 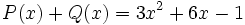 .
.
Dados los polinomios
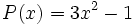 ;
; 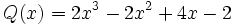
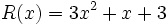 ;
; 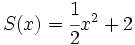
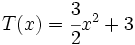 ;
; 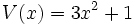
12a) Calcula P(x) + Q(x).
12b) Calcula P(x) - V(x).
12c) Calcula P(x) + R(x).
12d) Calcula P(x) - R(x).
12e) Calcula S(x) + T(x) + V(x).
12f) Calcula S(x) - T(x) + V(x).
13) Dados los polinomios
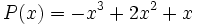 ;
; 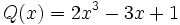
calcula el polinomio M(x) tal que P(x) + M(x) = Q(x).
17) La diferencia de dos polinomios es:
Calcula  sabiendo que
sabiendo que 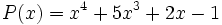 .
.
18) ¿Qué polinomio hay que sumar al polinomio 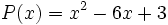 para obtener el polinomio opuesto de
para obtener el polinomio opuesto de 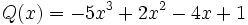 ?
?
19) Dados los polinomios:
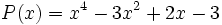 ;
; 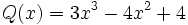 ;
; 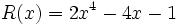
- 19a) Calcula P(x) + Q(x) - R(x)
- 19b) Calcula P(x) + R(x) - Q(x)
- 19c) Calcula Q(x) + R(x) - P(x)
- 19d) Calcula P(x) + Q(x) + R(x)
14) Escribe dos polinomios cualesquiera y súmalos. Contesta:
- 14a) ¿Es mayor el grado de los sumandos o el de la suma? ¿Es igual? ¿Es menor?
- 14b) ¿Puede en algún caso ser menor el grado de la suma que el de los sumandos? ¿Cuándo? Justifícalo con ejemplos.
15) ¿Qué puedes decir del grado de la diferencia de dos polinomios?
16) escribe dos polinomios de tercer grado de modo que su suma se el polinomio 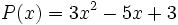 .
.
Determina el valor de "m" y "n" sabiendo que 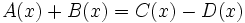 , en los siguientes casos:
, en los siguientes casos:
Actividades para aprender y practicar la suma y resta de polinomios.
Ejercicios para practicar la suma y resta de polinomios.
Suma de polinomios.
Resta de polinomios.
Suma y resta de polinomios.
Suma y resta de polinomios con dos variables.
Suma y resta de polinomios con dos variables.
Suma y resta de polinomios con dos variables: encuentra el error.
Suma de polinomios.
Resta de polinomios.
Ejercicios de autoevaluación sobre suma y resta de polinomios.
Producto de un monomio por un polinomio
Procedimiento
Para multiplicar un monomio por un polinomio, se aplica la propiedad distributiva, es decir, se multiplica el monomio por cada término del polinomio y se suman los resultados.
Aprende a multiplicar un monomio por un polinomio
Cómo se multiplica un polinomio por un monomio.
Multiplica y reduce:
- a)
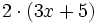
- b)
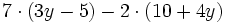
Expresa el área de la figura dada en el video como un trinomio.
Multiplica: 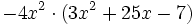
Averigua el valor de "c", "d" y "f" sabiendo que 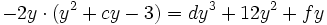
Multiplica:
- a)
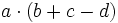
- b)
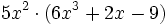
- c)
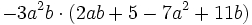
- d)
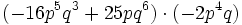
Haz las siguientes multiplicaciones de monomios:
- a)
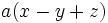
- b)
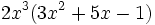
- c)
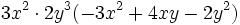
Calcula 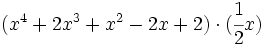
Calcula:
- 1c)
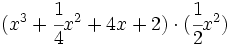
- 1d)
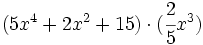
Actividades para aprender y practicar la multiplicación de un monomio por un polinomio.
Multiplicación de un número por un polinomio.
Multiplicación de monomios por polinomios.
Multiplicación de monomios por polinomios.
Multiplicación de monomios por polinomios.
Producto de polinomios
Procedimiento
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.
Aprende a multiplicar binomios
Aprende a multiplicar polinomios
En este tutorial se explica la multiplicación de monomios y polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.
Producto de monomios y polinomios en una variable.
Cómo se multiplican polinomios.
Propiedades conmutativa y asociativa del producto de polinomios.
Elemento neutro y distributiva en el producto de polinomios.
Producto de polinomios.
Producto de binomios:
Multiplica (x − 4)(x + 7).
Multiplica (3x + 2)(5x − 7).
Halla el área de la figura dada en el video, expresándola como el producto de dos binomios y como un trinomio.
Producto de binomios por polinomios:
Multiplica 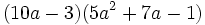 .
.
Halla el área de la figura dada en el video.
Halla el valor de "a" y "b" sabiendo que 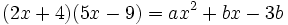 .
.
Producto de polinomios:
Multiplica:
- a)
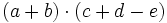
- b)
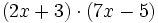
- c)
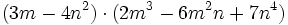
- d)
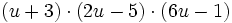
Multiplica:
- a)
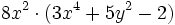
- b)
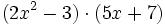
- c)
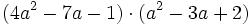
Determinar el polinomio que tiene por raíces: 2, 3 y -1, siendo la última raíz de multiplicidad 2.
Haz las siguientes multiplicaciones de polinomios:
- a)
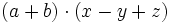
- b)
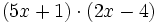
- c)
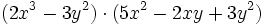
- d)
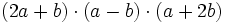
Dados los polinomios
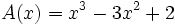 ;
; 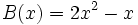 ;
; 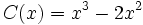
determina:
- a)
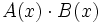
- b)
![C(x) \cdot [A(x)+ B(x)]\;](/wikipedia/images/math/e/0/8/e08fa9a42dff804cada0dd81daf805b8.png)
Multiplica los siguientes polinomios en columna e indicar el grado de los factores y del producto.
- 3a)
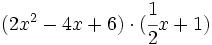
- 3b)
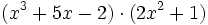
- 3c)
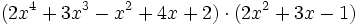
- 4a) Comprueba la propiedad conmutativa del producto de polinomios con los polinomios siguientes:
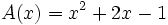 ;
; 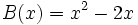
- 4b) Comprueba la propiedad asociativa del producto de polinomios con los polinomios siguientes:
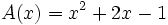 ;
; 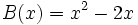 ; C(x)=x-2\;</math>
; C(x)=x-2\;</math>
- 5) Elemento neutro del producto de polinomios: Multiplica el polinomio
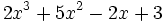 por el polinomio
por el polinomio 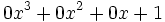 . ¿Qué polinomio obtienes?
. ¿Qué polinomio obtienes?
- 6a) Comprueba la propiedad conmutativa del producto de polinomios con los polinomios siguientes:
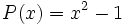 ;
; 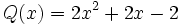
- 6b) Comprueba la propiedad asociativa del producto de polinomios con los polinomios siguientes:
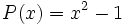 ;
; 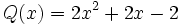 ;
; 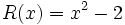
- 7a) Comprueba la propiedad distributiva del producto respecto de la suma de polinomios
![P(x) \cdot [Q(x)+R(x)]\;](/wikipedia/images/math/b/9/6/b96fc101039408c7ae1321f879455e95.png)
con los polinomios siguientes:
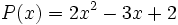 ;
; 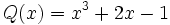 ;
; 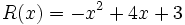
- 7b) Dados los polinomios
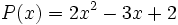 ;
; 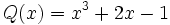
calcula
teniendo en cuenta que 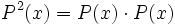 .
.
Dados los polinomios:
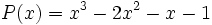 ;
; 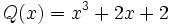 ;
;
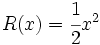 ;
; 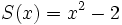
calcula:
- 8a)
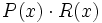
- 8b)
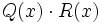
- 8c)
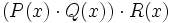
- 8d)
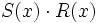
- 8e)
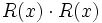
Dados los polinomios:
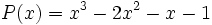 ;
; 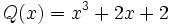 ;
;
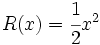 ;
; 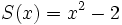
calcula:
- 8f)
![[P(x)]^2 \cdot R(x)\;](/wikipedia/images/math/2/3/e/23e83f298368c1a8c3119ea50a751be1.png)
- 8g)
![[Q(x)]^2\;](/wikipedia/images/math/f/c/0/fc0c585adb8c3eb99ba38d3006893145.png)
- 8h)
![[Q(x)]^2 \cdot S(x)\;](/wikipedia/images/math/5/d/c/5dce56fdbd0aef855ffaa69a67baf805.png)
calcula hallando previamente el grado de los factores y del producto:
- 9a)
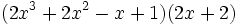
- 9b)
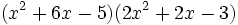
- 9c)
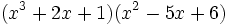
- 9d)
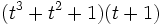
- 9e)
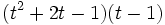
- 9f)
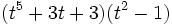
Calcula:
- 10a)
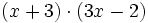
- 10b)
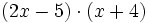
- 10c)
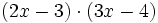
- 10d)
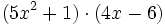
- 10e)
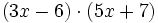
- 10f)
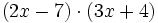
Completa:
- a) Si grado de P(x)=1 y grado de Q(x)=3, el grado de P(x)·Q(x) es ...
- b) Si grado de P(x)=2 y grado de Q(x)=4, el grado de P(x)·Q(x) es ...
- c) Si grado de P(x)=1 y grado de Q(x)=3, el grado de P(x)·Q(x) es ...
- d) Si grado de P(x)=6 y grado de Q(x)=1, el grado de P(x)·Q(x) es ...
Problemas:
Halla el volumen de un depósito cuya base tiene un área de 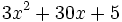 metros cuadrados y una altura de
metros cuadrados y una altura de 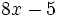 metros.
metros.
Escribe un binomio que exprese la diferencia entre el área de un rectángulo que mide "p" de largo y "2r" de ancho, y el área de un círculo cuyo diámetro mide 4r.
La parte de vidrio de una ventana tiene una proporción de 3:2 entre su largo y su ancho (la altura la podemos representar como 3x y la anchura como 2x). El marco de la ventana añade 7 cm al ancho total y 8 cm al alto total. Encuentra un polinomio, en términos de "x", que represente el área total de la ventana, incluyendo el marco.
Actividades para aprender y practicar la multiplicación de polinomios.
Multiplicación de binomios.
Multiplicación de binomios.
Multiplicación de binomios por polinomios.
Ejercicios de autoevaluación sobre producto de de polinomios.
|
Actividad: Operaciones con polinomios Haz las siguientes operaciones con polinomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2) b) expand (3x^3-5x^2-3x+2)*2x^2 c) expand (2x^2+2x-3)*(2x-5) |
División de monomios
Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Aprende a dividir monomios
Divide:
- a)
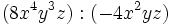
- b)
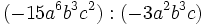
- c)
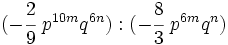
Divide los siguientes monomios:
- 54)
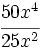 ; 55)
; 55) 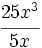 ; 56)
; 56) 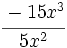 ; 57)
; 57) 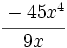
- 58)
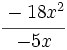 ; 59)
; 59) 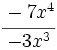 ; 60)
; 60) 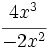 ; 61)
; 61) 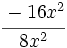
- 62)
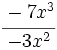 ; 63)
; 63) 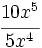 ; 64)
; 64) 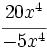 ; 65)
; 65) 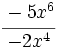
División de un polinomio entre un monomio
Para dividir un polinomio ente un monomio se divide cada uno de los monomios que componen el polinomio entre el monomio.
Aprende a dividir un polinomio entre un monomio
En este tutorial se explica la división de polinomios entre monomios.
Divide:
- a)
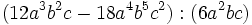
- b)
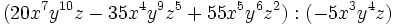
División de polinomios
La división polinómica es, en ciertos aspectos, similar a la división numérica.
Dados dos polinomios  (dividendo) y
(dividendo) y  (divisor) de modo que el grado de
(divisor) de modo que el grado de  sea mayor o igual que el grado de
sea mayor o igual que el grado de  y el grado de
y el grado de  sea mayor o igual a cero, siempre podremos hallar dos polinomios
sea mayor o igual a cero, siempre podremos hallar dos polinomios 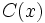 (cociente) y
(cociente) y 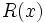 (resto) tales que:
(resto) tales que:
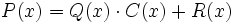
que también podemos representar como:
- El grado de
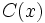 es igual a la diferencia entre los grados de
es igual a la diferencia entre los grados de  y
y  , mientras que el grado de
, mientras que el grado de 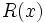 será, como máximo, un grado menor que
será, como máximo, un grado menor que  .
.
- Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.
División de polinomios. Ejemplos.
Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x).
Cómo se hace la división de polinomios
División de polinomios
Calcula:
a) 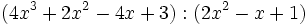
b) 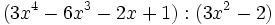
Calcula: 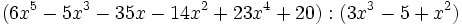
Calcula: 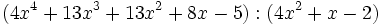
Calcula: 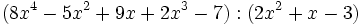
Calcula:
a) 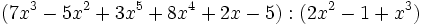
b) 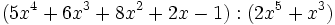
Calcula: 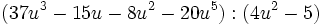
Divide los siguientes polinomios entre binomios:
- 1a)
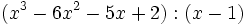
- 1b)
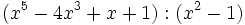
- 1c)
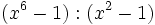
Divide los siguientes polinomios:
- 2a)
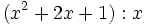
- 2b)
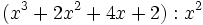
- 2c)
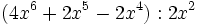
- 2d)
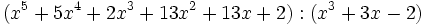
- 2e)
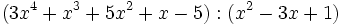
Divide los siguientes polinomios:
- 3a)
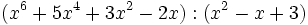
- 3b)
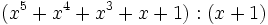
Divide los siguientes polinomios:
- 3c)
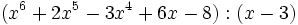
- 3d)
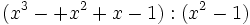
Divide los siguientes polinomios:
- 4a)
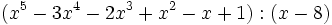
- 4b)
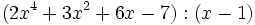
- 4c)
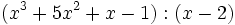
- 4d)
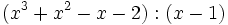
Divide los siguientes polinomios:
- 5a)
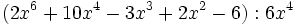
- 5b)
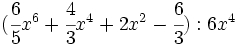
- 5c)
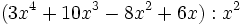
- 5d)
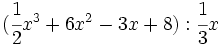
Divide los siguientes polinomios:
- 6a)
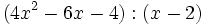
- 6b)
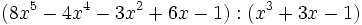
- 6c)
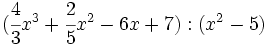
- 6d)
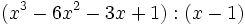
Indica qué divisiones de polinomios son exactas:
- 7a)
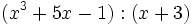
- 7b)
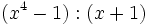
- 7c)
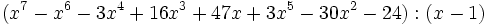
- 7d)
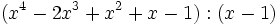
Divide los siguientes polinomios:
- 8a)
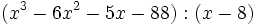
- 8b)
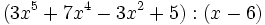
- 9a)
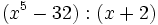
- 9b)
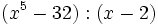
- 9c)
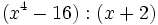
Divide los siguientes polinomios:
- 9d)
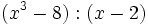
- 9e)
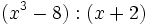
- 9f)
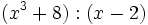
- 9g)
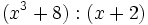
- 9h)
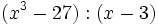
- 9i)
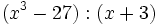
- 9j)
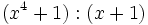
Divide los siguientes polinomios:
- a)
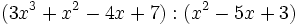
- b)
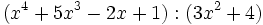
Método de Horner para la división de polinomios
Calcula: 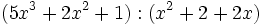
Halla el resto de la división:
Halla el resto de la división
sabiendo que la suma de los coeficientes del cociente es 28.
Ejercicios de autoevaluación sobre división de polinomios.