Funciones lineales (1º ESO)
De Wikipedia
| Revisión de 08:18 19 abr 2020 Coordinador (Discusión | contribuciones) (→Función lineal) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Función lineal) |
||
| Línea 45: | Línea 45: | ||
| |sinopsis=Representación gráfica de funciones lineales con Geogebra. | |sinopsis=Representación gráfica de funciones lineales con Geogebra. | ||
| }} | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejemplo | ||
| + | |duracion=13'33" | ||
| + | |url1=https://youtu.be/SPns94OMuA4 | ||
| + | |sinopsis=Ejemplo de la vida real. | ||
| + | }} | ||
| + | |||
| ---- | ---- | ||
| {{Video_enlace_profealex | {{Video_enlace_profealex | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Función de proporcionalidad
Una función de proporcionalidad directa es aquella cuya expresión analítica puede expresarse como:
 |
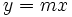es la variable independiente.
es la variable dependiente.
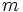una constante que se denomina constante de proporcionalidad o pendiente.
Representación gráfica
- La gráfica de una función de proporcionalidad directa es una recta que pasa por el origen de coordenadas.
- En consecuencia, para representarla sólo necesitamos un punto y el origen, los cuales uniremos mediante una línea recta. Para obtener dicho punto usaremos la ecuación.
Ejemplo: Función de proporcionalidad directa
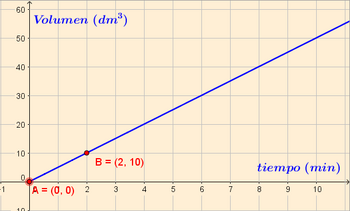
Un grifo, con un caudal de 5 dm3 por minuto, vierte agua en una piscina.
- a) Haz una tabla de valores de la función que relaciona el tiempo con el volumen que se llena.
- b) Halla la expresión analítica de la función.
- c) Representa gráficamente la función.
Solución:
- La variable independiente es el tiempo transcurrido y la dependiente el volumen que ocupa el agua vertida en ese tiempo.
- a) Tabla de valores:
| tiempo (min) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Volumen (dm3) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
- b) Expresión analítica:
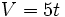(V en dm3; t en minutos)
- c) Representación gráfica: Como se trata de una función de proporcionalidad directa, su gráfica es una recta que pasa por el origen. Por tanto, solo tendremos que representar un punto y el origen, y unirlos mediante una línea recta.
- Sólo se representan los valores
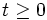, ya que el tiempo empieza a contar a partir de cero.
Tutorial (2´11") Sinopsis:Función de proporcionalidad directa. Expresión analítica y gráfica.
Ejemplo 1a (2´11") Sinopsis: Variable independiente y dependiente en una función de proporcionalidad directa dada por una ecuación y su correspondiente tabla.
Ejemplo 1b (1´01") Sinopsis: Ejemplo de representación gráfica de una función de proporcionalidad directa dada por una ecuación y su correspondiente tabla.
Ejemplo 1c (2´02") Sinopsis: Ejemplo sobre la obtención de la ecuación de una función de proporcionalidad directa a partir de su gráfica y de su correspondiente tabla.
Función de proporcionalidad directa Descripción: En esta escena podrás ver e interactuar con las gráficas de funciones de proporcionalidad directa y estudiar sus propiedades.
Actividad 1 Descripción: La función de proporcionalidad directa. Ejemplos.
Actividad 2 Descripción: Ejercicio sobre funciones de proporcionalidad directa.
Función lineal
Una función lineal es aquella cuya expresión analítica puede expresarse como:
 |
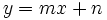- es la variable independiente.
- es la variable dependiente.
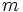- es una constante que se denomina pendiente.
es otra constante denominada ordenada en el origen. (Si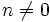 
recibe el nombre de función afín)
Función lineal Descripción: En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades.
Tutorial (8'23") Sinopsis: Representación gráfica de funciones lineales.
Representación gráfica de funciones lineales con Geogebra (14'58") Sinopsis:Representación gráfica de funciones lineales con Geogebra.
Ejemplo (13'33") Sinopsis:Ejemplo de la vida real.
Ejercicio 1a (7'22") Sinopsis: Representación gráfica de y=3x-2.
Ejercicio 1b (8'47") Sinopsis: Representación gráfica de -4x+2y=6.
Ejercicio 1c (9'53") Sinopsis: Representación gráfica de 3y-2x=4.
Ejercicio 2 (9'10") Sinopsis:Representación gráfica de y=3x+2 y de 4+y=2x.
Actividad 1 Descripción: Ejemplo de función lineal.
Actividad 2a Descripción: Ejercicio sobre funciones lineales.
Actividad 2b Descripción: Ejercicio sobre funciones lineales.
Actividad 2c Descripción: Ejercicio sobre funciones lineales.
Autoevaluación 1 Descripción: Identifica ecuaciones de rectas a partir de sus gráficas.
Autoevaluación 2 Descripción: Problemas sobre ecuaciones, tablas y gráficas de funciones lineales.
Autoevaluación 3 Descripción: Ejercicios sobre funciones lineales.
