Interés compuesto
De Wikipedia
| Revisión de 17:25 18 sep 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:32 18 sep 2007 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Al depositar una cantidad de dinero C en una entidad bancaria, genera al cabo del tiempo unos beneficios llamados '''intereses'''. Supongamos que el tipo de interés o '''rédito''' pactado sea r% anual, entonces al ser un problema de encadenamiento de aumento porcentual, el capital final o acumulado en '''n''' años será: | Al depositar una cantidad de dinero C en una entidad bancaria, genera al cabo del tiempo unos beneficios llamados '''intereses'''. Supongamos que el tipo de interés o '''rédito''' pactado sea r% anual, entonces al ser un problema de encadenamiento de aumento porcentual, el capital final o acumulado en '''n''' años será: | ||
| Línea 14: | Línea 15: | ||
| |enunciado= a) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años? | |enunciado= a) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años? | ||
| - | b) a) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años, si el periodo de capitalización es mensual (paga los intereses cada mes)? | + | b) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años, si el periodo de capitalización es mensual (paga los intereses cada mes)? |
| |sol= a) <math> C_F=10000.1,06^5=13382,26</math>€ | |sol= a) <math> C_F=10000.1,06^5=13382,26</math>€ | ||
| - | b) | + | b)Al ser el 6% anual, el tanto por ciento mensual será 6/12=0,5% y el número de meses en 5 años es 12.5 = 60 meses. Aplicando el encadenamiento de aumento porcentual, tenemos: |
| + | <math> C_F=10000.1,005^60=13488,50</math>€. Como se puede deducir el periodo de capitalización mensual es mucho más favorable para el cliente. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:32 18 sep 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Al depositar una cantidad de dinero C en una entidad bancaria, genera al cabo del tiempo unos beneficios llamados intereses. Supongamos que el tipo de interés o rédito pactado sea r% anual, entonces al ser un problema de encadenamiento de aumento porcentual, el capital final o acumulado en n años será:
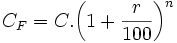
Ejemplo: Cálculo del capital final
a) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años?
b) ¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años, si el periodo de capitalización es mensual (paga los intereses cada mes)?
a) CF = 10000.1,065 = 13382,26€
b)Al ser el 6% anual, el tanto por ciento mensual será 6/12=0,5% y el número de meses en 5 años es 12.5 = 60 meses. Aplicando el encadenamiento de aumento porcentual, tenemos:
CF = 10000.1,00560 = 13488,50€. Como se puede deducir el periodo de capitalización mensual es mucho más favorable para el cliente.
