Funciones: Expresión analítica

(Diferencia entre revisiones)

Revisión de 16:06 22 abr 2008

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Coordenadas Funciones (SM)	Trazando gráficas Ejercicios 1 Ejercicios 2	WIRIS Geogebra Calculadora Función Lista de funciones

La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.

Ejemplos:

a) El área de un rectángulo que mide 2 cm más de largo que de ancho, viene dada por la expresión analítica: 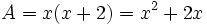$A=x(x+2)=x^2+2x\;\!$

b) El perímetro de ese mismo rectángulo vendrá dado por: 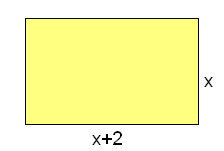$P=2x+2(x+2)=4x+4 \;\!$

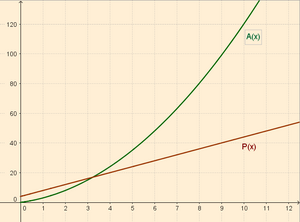
Realizamos una tabla de datos para caso y dibujamos dichos puntos quedando la función área como la gráfica azul y el perímetro como la gráfica verde:

Actividad Interactiva: Expresión analítica de una función

Actividad 1: Expresión analítica de una función cuya gráfica es una recta.

Actividad:

Imagínate que trabajas como representante de una empresa que se dedica a la creación de juegos para ordenador. Tu sueldo es de 300 euros fijos cada mes, más 3 euros por juego que has vendido. ¿Qué magnitudes se relacionan? ¿Son todas variables?.
Construye, en tu cuaderno de trabajo, una tabla de valores que recoja el sueldo que cobrarías, en función del número de videojuegos que hayas vendido. Por cuestiones prácticas los datos se representan en ventas de 5 en 5 juegos.
Dibuja la gráfica que ha ido apareciendo en la escena. ¿Qué tipo de gráfica es?. Intenta escribir una relación que te permita conocer, de antemano, el sueldo que te pagarán conocida la cantidad de juegos que has vendido a lo largo del mes.
Si durante el último mes has vendido 347 juegos, ¿qué sueldo cobrarás? Si un mes te pagaron 714 euros, ¿cuántos juegos vendiste?
Comprueba el proceso en la siguiente escena:

Click aquí si no se ve bien la escena

Actividad 1: Expresión analítica de una función cuya gráfica es una parábola.

Actividad:

La gráfica que verás aparecer en la escena hace referencia a la siguiente cuestión: Unos alumnos de ESO disponen de una cuerda de 24 metros de longitud. Con ella deben construir rectángulos en el patio de su centro. Haz una tabla de valores donde se relacione la base de los rectángulos y su área.
Halla una expresión que te permita calcular el área de cualquiera de esos rectángulos, conocida su base.
Comprueba el proceso en la siguiente escena:

Click aquí si no se ve bien la escena

 b) El perímetro de ese mismo rectángulo vendrá dado por: <math>P=2x+2(x+2)=4x+4 \;\!</math>
 |celda2=[[Imagen:rectangulo2.png]]}}
-[[Imagen:graficas.png]]
+{{p}}
+Realizamos una tabla de datos para caso y dibujamos dichos puntos quedando la función área como la gráfica azul y el perímetro como la gráfica verde:
+<center>
+[[Imagen:graficas.png|300px]]
+</center>
 }}