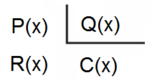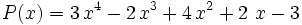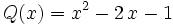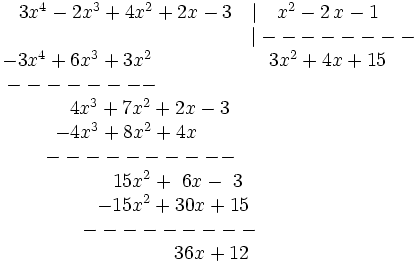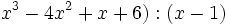Plantilla:División de polinomios
De Wikipedia
La división polinómica es, en ciertos aspectos, similar a la división numérica.
Dados dos polinomios 
(dividendo) y 
(divisor) de modo que el grado de sea mayor o igual que el grado de y el grado de sea mayor o igual a cero, siempre podremos hallar dos polinomios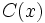 
(cociente) y 
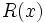(resto) tales que:
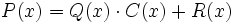
que también podemos representar como:
- El grado de 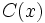es igual a la diferencia entre los grados de y , mientras que el grado de 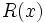será, como máximo, un grado menor que .
- Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.
Ejemplo: División de polinomios
Divide los siguientes polinomios:
Actividad: División de polinomios Calcula el cociente y el resto de la siguiente división de polinomios:  Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: quotient and remainder (x^3-4x^2+x+6)/(x-1) |
Ejempo: División entre polinomios (10'30") Sinopsis: Divide: 
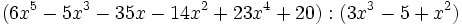
División de polinomios (9´) Sinopsis:Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x).
2 ejemplos de división de polinomios (12´) Sinopsis:Videotutorial.
