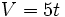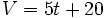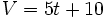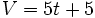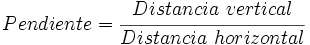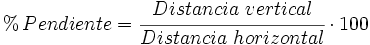Función lineal (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 166)
Función lineal
Una función lineal es aquella cuya expresión analítica puede expresarse como:
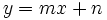 |
 es la variable independiente.
es la variable independiente.
 es la variable dependiente.
es la variable dependiente.
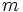 es una constante que se denomina pendiente.
es una constante que se denomina pendiente.
 es otra constante denominada ordenada en el origen. (Si
es otra constante denominada ordenada en el origen. (Si 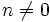 recibe el nombre de función afín)
recibe el nombre de función afín)
Representación gráfica
- La gráfica de una función lineal es una recta que corta al eje de ordenadas en el punto
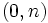 .
.
- En consecuencia, para representarla, necesitamos dos puntos, uno de los cuales puede ser el
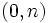 . El otro punto se obtendrá a partir de la ecuación.
. El otro punto se obtendrá a partir de la ecuación.
Ejemplo: Función lineal
- Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados.
- Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros.
- ¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados?
- Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian.
- ¿Qué fórmula correspondería a esta situación gráfica?
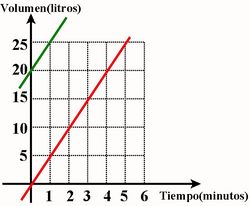
| 2. Supongamos ahora que el estanque tiene inicialmente un volumen de 20 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
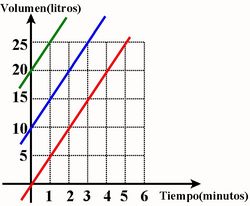
| 3. Ahora supondremos que el estanque tiene inicialmente un volumen de 10 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
4. Las graficas son rectas paralelas que cortan al eje de ordenadas a una altura que coincide con el volumen inicial del estanque. Por tanto, tienen en común que tienen la misma inclinación y se diferencian en el punto de corte con el eje de ordenadas.
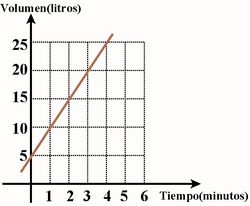
5. Para esta gráfica que corta al eje de ordenadas en 5, la fórmula que expresa la relación entre el volumen y el tiempo es:
| 
|
En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades.
Tutorial en el que se explican los conceptos básicos y propiedades de las funciones lineales, así como su representación gráfica.
Representación gráfica de funciones lineales.
Representación gráfica de funciones lineales con Geogebra.
Tutorial en el que se explican los conceptos básicos y propiedades de las funciones lineales, así como su representación gráfica.
Representa gráficamente la función 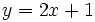 .
.
Representa gráficamente la función 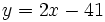 a partir de sus puntos de corte
a partir de sus puntos de corte
Representa gráficamente las funciones:
a) 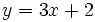
b) 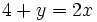
c) 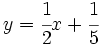
Definición de función lineal. Ejemplos.
Actividades en las que aprenderás a representar funciones lineales y a identificar su ecuación a partir de su gráfica.
Ejercicio sobre funciones lineales.
Ejercicio sobre funciones lineales.
Ejercicio sobre funciones lineales.
Identifica ecuaciones de rectas a partir de sus gráficas.
Problemas sobre ecuaciones, tablas y gráficas de funciones lineales.
Ejercicios sobre funciones lineales.
Representación gráfica de la función lineal
Representación gráfica
- La gráfica de una función lineal es una recta que corta al eje de ordenadas en el punto
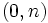 .
.
- En consecuencia, para representarla, necesitamos dos puntos, uno de los cuales puede ser el
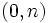 . El otro punto se obtendrá a partir de la ecuación.
. El otro punto se obtendrá a partir de la ecuación.
Ejemplo: Función lineal
- Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados.
- Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros.
- ¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados?
- Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian.
- ¿Qué fórmula correspondería a esta situación gráfica?
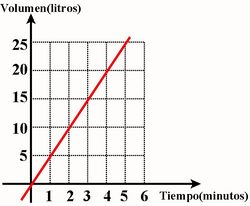
| 1. Un estanque tiene un grifo que vierte 5 litros por minuto.
Partimos de que el estanque se encuentra vacío inicialmente. Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo es:
| 
|
| 2. Supongamos ahora que el estanque tiene inicialmente un volumen de 20 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
| 3. Ahora supondremos que el estanque tiene inicialmente un volumen de 10 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
4. Las graficas son rectas paralelas que cortan al eje de ordenadas a una altura que coincide con el volumen inicial del estanque. Por tanto, tienen en común que tienen la misma inclinación y se diferencian en el punto de corte con el eje de ordenadas.
5. Para esta gráfica que corta al eje de ordenadas en 5, la fórmula que expresa la relación entre el volumen y el tiempo es:
| 
|
Pendiente de una función lineal
Concepto de pendiente
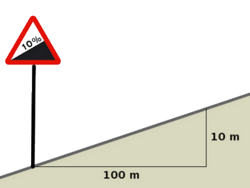
En topografía, la pendiente es la relación que existe entre el desnivel, o distancia en vertical, que debemos superar y la distancia en horizontal que debemos recorrer:
|
Una rampa con un ángulo de inclinación de 45º tiene una pendiente del 100%, ya que el triángulo formado por la rampa es isósceles.
Este concepto topográfico de pendiente tiene mucho que ver con el concepto de pendiente de una función lineal si consideramos la recta, su gráfica, como si fuese una rampa. No obstante, la pendiente de una función lineal puede tomar valores negativos, mientras que la pendiente topográfica siempre es positiva, como podrás comprobar en la siguiente actividad interactiva.
Concepto de pendiente. En la escena podrás calcular la pendiente de una rampa.
Escena en la que podrás practicar el cálculo de la pendiente a partir de una gráfica.
Escena en la que podrás practicar dibujando una gráfica que tenga una pendiente dada.
Cálculo de la pendiente de una recta
Proposición
Consideremos una función lineal 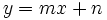 y dos puntos
y dos puntos 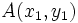 y
y 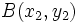 de la recta que la representa.
de la recta que la representa.
La pendiente se puede calcular de la siguiente manera:
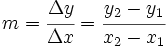
Como 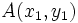 es un punto de la recta, verifica su ecuación:
es un punto de la recta, verifica su ecuación: 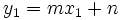
Como 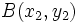 es otro punto de la recta, también verifica su ecuación:
es otro punto de la recta, también verifica su ecuación: 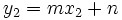
Restando ambas expresiones:
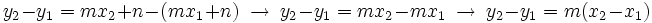
y despejando m:
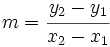
- En este vídeo se explica como se calcula la pendiente de una recta.
- También se resolverá el siguiente problema: Los vértices de un triángulo son los puntos (2,-2), (-1,4) y (4,5). Halla la pendiente de cada uno de sus lados.
Introducción a la pendiente de una recta.
Ejemplos de cálculo de la pendiente de una recta a partir de su gráfica.
Encuentra la pendiente de la recta que pasa por los puntos (4,2) y (-3, 16).
Encuentra la pendiente de la recta dada en el video.
Halla la pendiente de la recta que pasa por los puntos (7,-1) y (-3,-1).
Halla la pendiente de la recta que pasa por los puntos P(2,7) y Q(-2,3).
Pendiente de una recta.
Escena en la que aprenderás a calcular la pendiente de una función lineal.
Practica el cálculo de la pendiente de una función lineal a partir de dos puntos.
La pendiente a partir de dos puntos.
La pendiente a partir de una gráfica.
La pendiente y el crecimiento
Propiedades
La pendiente,  , describe el crecimiento de la función
, describe el crecimiento de la función 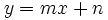 :
:
- Si
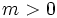 , la función es creciente.
, la función es creciente.
- Si
 la función es decreciente.
la función es decreciente.
- Si
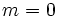 la función es constante (recta horizontal).
la función es constante (recta horizontal).
Además, cuanto mayor es su pendiente (en valor absoluto), más inclinada es su gráfica.
Pendiente de una recta. Significado del signo de la pendiente.
En esta escena podrás ver como afecta el signo de la pendiente al crecimiento de la función lineal.
Obtención de la función lineal a partir de su gráfica
Procedimiento
Para determinar la ecuación de una función lineal a partir de su gráfica seguiremos uno de los dos procedimientos siguientes:
Procedimiento 1:
- Localizaremos en la gráfica el punto de corte con el eje Y,
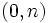 , para averiguar el valor del parámetro
, para averiguar el valor del parámetro  .
.
- Localizaremos otro punto de la recta cuyas coordenadas sean conocidas.
- Con esos dos puntos calcularemos la pendiente:
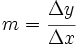 .
.
- Una vez averiguados
 y
y  , los sustituiremos en la ecuación
, los sustituiremos en la ecuación 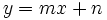 .
.
Procedimiento 2:
- Si no fuera posible determinar el punto de corte con el eje Y,
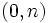 , localizaremos en la gráfica dos puntos de la recta cuyas coordenadas sean conocidas.
, localizaremos en la gráfica dos puntos de la recta cuyas coordenadas sean conocidas.
- Con esos dos puntos calcularemos la pendiente:
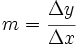 .
.
- Una vez averiguada
 , sustituiremos las coordenadas de uno de los dos puntos en la ecuación
, sustituiremos las coordenadas de uno de los dos puntos en la ecuación 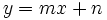 y despejaremos
y despejaremos  .
.
Estos procedimientos sólo funcionan si la gráfica nos permite determinar los puntos de los apartados 1 y 2.
Obtención de la función afín a partir de su gráfica.
Obtención de la función afín a partir de su gráfica. Ejemplos.
Halla la ecuación de la recta a partir de la gráfica dada.
Halla el valor de a a partir de la información dada en la gráfica.
Problema sobre funciones lineales.
Aprende a obtener la ecuación de una función afín a partir de su gráfica.
En esta escena podrás practicar aprender como se obtiene la ecuación de la función lineal a partir de su gráfica.
En esta escena podrás practicar con ejercicios en los que se trata de obtener la ecuación de la función lineal a partir de su gráfica.
Aprende a obtener la ecuación de una función afín a partir de su gráfica.
Análisis de una función lineal
Análisis de una función lineal: Dominio, rango, puntos de corte y crecimiento.
Ejercicios
|
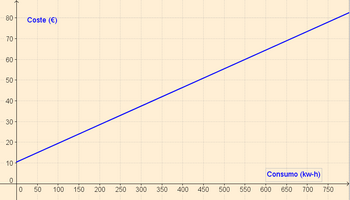
Ejercicio resuelto: Modelado de una función lineal La factura de la luz que hemos contratado en casa nos supone un coste fijo mensual de 10,44 €, además de 0,09 € por kilovatio-hora consumido.
|
Ejercicios propuestos
|
Ejercicios propuestos: Función lineal |