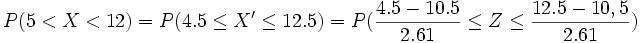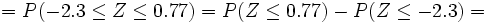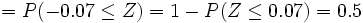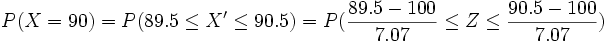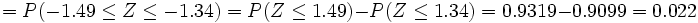La distribución normal
De Wikipedia
Tabla de contenidos |
Definición
Entre las distribuciones continuas la más importante es la llamada distribución normal.
Fue introducida por Carl Friedrich Gauss a principios del siglo XIX en su estudio de los errores de medida. Desde entonces se ha utilizado como modelo en multitud de variables (peso, altura, calificaciones...), en cuya distribución los valores más usuales se agrupan en torno a uno central y los valores extremos son escasos.
Una variable aleatoria continua sigue una distribución normal si su función de densidad es:
|
|
donde 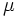 y
y 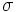 coinciden respectivamente con la media y la desviación típica de la variable aleatoria. Estos parámetros son los que determinan esta distribución que designaremos por N(μ,σ)
coinciden respectivamente con la media y la desviación típica de la variable aleatoria. Estos parámetros son los que determinan esta distribución que designaremos por N(μ,σ)
|
Actividades Interactivas: La Campana de Gaus
Actividad 1. Propiedades de la curva normal
Actividad: La gráfica de esta función tiene forma de campana y se conoce con el nombre de campana de Gauss. Observa que la forma de la campana y la situación respecto a los ejes dependen de los parámetros m (μ) y s (σ) ¿Qué características tiene la normal de media 0 y desviación típica 1?. Descríbelas. Cambia el valor de la media m y la desviación típica s en esta distribución normal y observa lo que ocurre. |
Tabla N(0,1)
En la tabla N(0,1) aparece directamente la 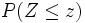 para valores de z entre 0 y 4. Observa que para valores mayores que 4 la probabilidad ya es prácticamente 1.
para valores de z entre 0 y 4. Observa que para valores mayores que 4 la probabilidad ya es prácticamente 1.
Manejo de la tabla
|
Actividades Interactivas: Cálculo de probabilidades N(0,1)
Actividad 1.Tipo I:
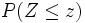 Actividad: Mirando en la tabla N(0,1) y comprobando en la escena que estas probabilidades se obtienen directamente de la tabla, siendo la casilla donde se cruza la fila de las unidades y décimas de z, con la columna de las centésimas de z. a) Identifica sobre el gráfico (puedes usar los colores): ¿dónde se representan los valores de la variable de los que estamos calculando la probabilidad? ¿cómo se representa esa probabilidad? b) Da distintos valores, z, a la variable y busca su probabilidad acumulada en la tabla de la normal que aparece anteriromente. Puedes comprobar la corrección de lo que has hecho comparando tu resultado con el valor que aparece en el gráfico, aunque fíjate que la tabla da los resultados con una precisión mayor que el gráfico (que aproxima sólo hasta las milésimas). c) Calcula, en particular, la probabilidad acumulada de 0.5, 1, 1.64, 1.96, 2, 2.58, ... d) Recuerda que la curva normal es la función de densidad de una variable normal; por tanto, ¿cuál es el área total bajo la curva?
Actividad 2.Tipo II:
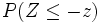 Actividad: Mirando en la tabla N(0,1) y comprobando en la escena que se cumple 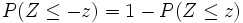
Actividad 3.Tipo III:
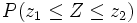 Actividad: Mirando en la tabla N(0,1) y comprobando en la escena que se cumple 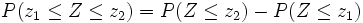
|
Tipificación
Como ya debes saber, para calcular probabilidades con variables que siguen la distribución normal se usan tablas. Pero, puesto que sería imposible tener una tabla para cada posible distribución normal, como habrás visto en el apartado anterior, solamente tenemos la tabla de la distribución normal estándar. Necesitamos, ser capaces de transformar las variables 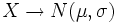 que encontremos, en variables
que encontremos, en variables 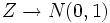 . Este proceso se llama tipificación de la variable.
. Este proceso se llama tipificación de la variable.

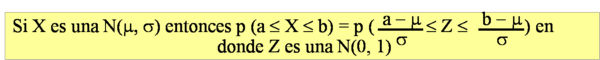
|
Ejercicios: Cálculo de probabilidades 1. Calcula: a) En N(10,5); b) En N(9,3); P(X > 15) c) En N(12,5); d) En N(10;3,5); 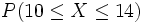 Solución: a) 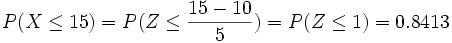
c)
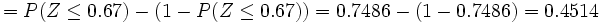
2. Las estaturas de cierta población se distribuyen según una normal de media 168 y desviación típica 8. Calcula la probabilidad de que elegida una persona al azar su altura sea 170 cm. como máximo.
Solución: La población es N(168,8) Hemos de calcular la probabilidad
Calculamos el valor tipificado 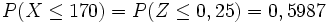
3. Las notas de cierto examen se distribuyen según una normal de media 5,4 y desviación típica 1,2. ¿Qué porcentaje de estudiantes se puede esperar que sacasen entre 5 y 7?
Solución: 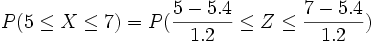
|
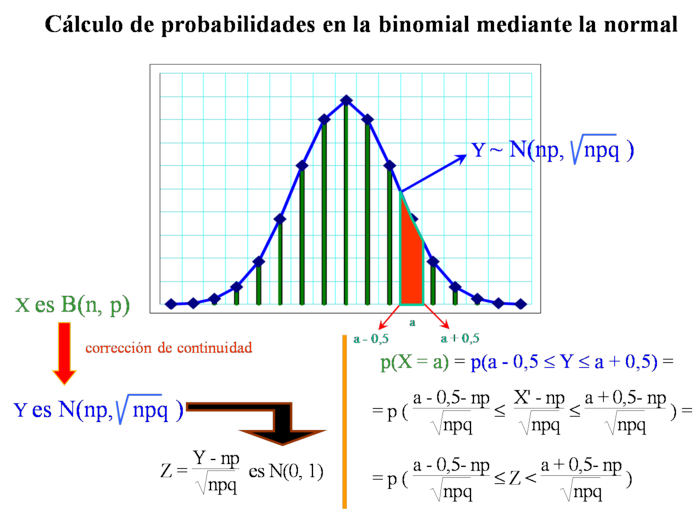
Aproximación de una binomial por una normal
|
Ejercicios: Cálculo de probabilidades de las binomiales 1. El 35% de una población está afectado por la gripe. Se eligen 30 personas al azar. Calcula la probabilidad de que: a) haya exactamente 10 enfermos. b) haya más de 5 y menos de 12 enfermos. Se trata de una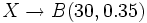 se aproxima a se aproxima a 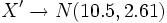 Solución: a) 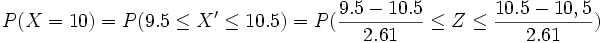
b)
![P(Z \le 0.77) - [1-P(Z \le 2.3)]=0.7794-1+0.9893 =0.7687](/wikipedia/images/math/3/a/4/3a4e765de52f7abde3ceb070f9fe2a09.png) 2. Se lanza una moneda 200 veces: a) Calcula la probabilidad de que aparezca cara al menos 100 veces. b) ¿Cuál es la probabilidad de que aparezcan 90 caras? Se trata de una No se pudo entender (error de sintaxis): X \rightarrow B(200, \frac{1} {2}}) se aproxima a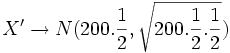 Solución: a) 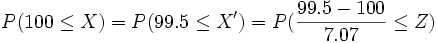
b)
|

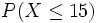
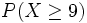
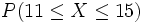
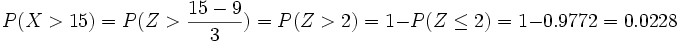
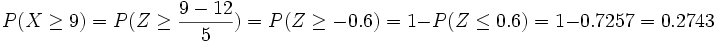
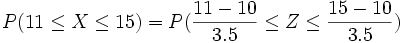
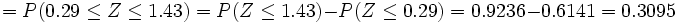
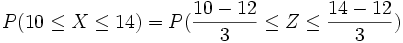
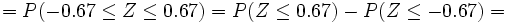
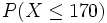
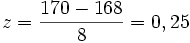 y buscamos en la tabla N(0,1) la probabilidad correspondiente:
y buscamos en la tabla N(0,1) la probabilidad correspondiente:
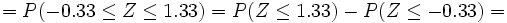
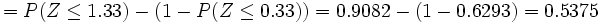
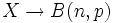 se aproxima a
se aproxima a 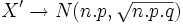
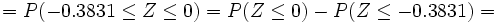
![P(Z \le 0) - [1-P(Z \le 0.3831)]= 0.5 - 1 + P(Z \le 0.3831)=-0.5 + 0.648 = 0.148](/wikipedia/images/math/a/b/a/ababb1f6aaf6a8279dd9210a9ce9e5f1.png)