Raíces de un polinomio (4ºESO Académicas)

De Wikipedia

Revisión de fecha 08:35 1 oct 2018; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Menú:

Enlaces internos	Para repasar	Enlaces externos
Indice Descartes Manual Casio	Test de Álgebra	WIRIS Calculadora

[editar]

Raíces de un polinomio

Un número $a\,$ es una raíz o un cero de un polinomio $P(x)\,$ , si $P(a)\, = 0\,$ .

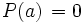Dicho de otra forma, las raíces de un polinomio son las soluciones de la ecuación 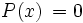$P(x)\,= 0\,$ .

Raíces de un polinomio (8'40") Sinopsis:

Raíces de un polinomio. Ejemplos.

Teorema del factor

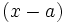$x=a\;$ es una raíz de un polinomio $P(x)\;$ si y solo si $(x-a)\;$ es un factor de dicho polinomio.

Demostración:

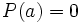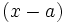En efecto, si $x=a\;$ es una raíz de $P(x)\;$ , entonces $P(a)=0\;$ y, por el teorema del resto, el resto de dividir $P(x)\;$ entre $(x-a)\;$ es cero. Así 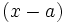$(x-a)\;$ es un factor de $P(x)\;$ .

El recíproco es trivial.

[editar]

Raíces enteras de un polinomio

Supongamos que tenemos un polinomio 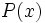$P(x)\,\!$ con coeficientes enteros y del cual sabemos que sus raíces son también números enteros. ¿Cómo las encontramos?. Para hacerlo tendríamos que ir probando a dividirlo por 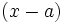$(x-a)\,\!$ , pero ¿qué valor puede tomar 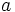$a\,\!$ ? El siguiente resultado nos da la respuesta:

Teorema

Las raíces enteras de un polinomio con coeficientes enteros son divisores de su término independiente.

Demostración:

Demostración:

En efecto, sea $x=a\;$ una raíz entera de un polinomio con coeficientes enteros

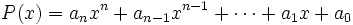
$P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$

Entonces, como 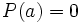$P(a)=0\;$ , tendremos que

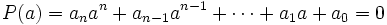
$P(a)=a_na^n+a_{n-1}a^{n-1}+\cdots+a_1a+a_0=0$

de donde, despejando el termino independiente

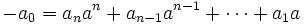
$-a_0=a_na^n+a_{n-1}a^{n-1}+\cdots+a_1a$

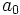Como el miembro de la derecha contiene al factor $a\;$ en todos sus sumandos, es un múltiplo de $a\;$ , entonces $a_0\;$ también. Luego $a\;$ divide al término independiente.

[editar]