Perímetros y áreas
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Áreas Áreas y perímetros | Ejercicios | WIRIS Geogebra Calculadora Polígonos Círculo |
Tabla de contenidos |
Cuadrado

|
|
|
|
Actividad interactiva: Cuadrado
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro de un cuadrado
(Mueve el vértice del cuadrado para variar la medida del lado)
|
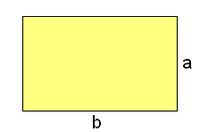
Rectángulo
|
|
|
|
Actividad interactiva: Rectángulo
1. La base de un rectángulo es 5 m. y la altura la mitad de la base. Calcula el área y el perímetro.
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro de un rectángulo
(Mueve los vértices del rectángulo para variar la medida de los lados)
|
Paralelogramo

|
|
|
|
Actividad interactiva: Paralelogramo
1. Deducción de las fórmulas del área y del perímetro del paralelogramo.
Actividad: El paralelogramo de la derecha tiene el mismo área que el rectángulo que tiene debajo. Para comprobarlo, mueve el punto que se indica y arrastralo hacia la izquierda. Por tanto el área del paralelogramo es el mismo que el del rectángulo. Deducción de las fórmulas del área y del perímetro del paralelogramo
(Mueve el punto azul)
2. La base de un paralelogramo es 5 cm, y su altura es 2,8 cm. ¿Cual es el área y el perímetro del paralelogramo?
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro del paralelogramo
(Mueve los vértices para modificar la medida de los lados)
|
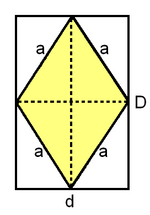
Rombo
|
|
|
|
Actividad interactiva: Rombo
1. La diagonal mayor de un rombo mide 5m, y la menor es la mitad. Calcula el área y el perímetro del rombo.
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro del rombo
(Mueve los vértices para modificar la medida de los lados)
2. Calcula el área de un cuadrado de 4 m. de diagonal.
|
Triángulo
|
|
|
Actividad interactiva: Triángulo
1. Cálculo del área y perímetro de un triángulo.
Actividad: En esta escena puedes calcular el área y el perímetro de un triángulo. Mueve los vértices del triángulo para variar la medida de los lados. Contesta en tu cuaderno y comprueba los resultados en la escena anterior:
|
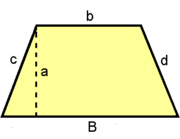
Trapecio
|
|
|
|
Actividad interactiva: Trapecio
1. Deducción de la fórmula del área de un trapecio.
Actividad: Para ello, mueve el punto rojo hacia la izquierda. Obtendrás un duplicado del trapecio en color azul, que junto con el trapecio amarillo inicial, forman un paralelogramo de base 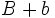 y altura y altura  . .
El área del paralelogramo es: 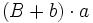 de donde, dividiendo por 2, obtenemos el área del trapecio: 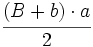
2. Halla el área y el perímetro de un trapecio de base mayor 5 cm., base menor 1,5 cm. y altura 2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: (Mueve los vértices del trapecio para variar la medida de los lados)
3. Halla el área y el perímetro de un trapecio rectángulo de base mayor 4,5 cm., base menor 3 cm. y altura 1,2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: (Mueve los vértices del trapecio para variar la medida de los lados)
4. Halla el área y el perímetro de un trapecio isósceles de base mayor 4 cm., base menor 2,4 cm. y lado L=2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: (Mueve los vértices del trapecio para variar la medida de los lados) |
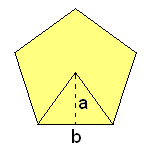
Polígonos regulares
|
|
|
|
Actividad interactiva: Polígono regular
1. Cálculo del área y perímetro de un polígono regular.
Actividad: En esta escena puedes calcular el área y el perímetro de un polígono regular. Mueve los puntos azules para variar el número de lados y la medida de los mismos. Pero, para determinar el área, necesitamos conocer, además del lado, la apotema. Si conocemos uno de ellos y el radio, podemos hallar el otro por el Teorema de Pitágoras, como se observa en la siguiente escena: Contesta en tu cuaderno y comprueba los resultados en las escenas anteriores:
|
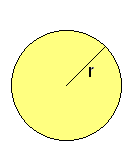
Círculo
|
|
|
|
Actividad interactiva: Círculo
1. En un círculo de radio 1,71 cm, halla su área y la longitud de su circunferencia.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: |
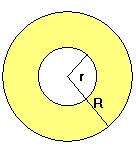
Corona circular
|
|
|
|
Actividad interactiva: Corona circular
1. Halla el área de una corona circular cuyos círculos tienen de radio 2 cm y 1,37 cm, respectivamente.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Mueve el punto azul para modificar el radio pequeño |
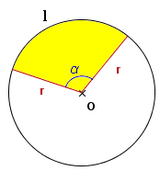
Sector circular
|
|
|
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
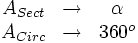
Despejando el área del sector:
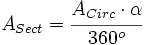
de donde, sustituyendo el área del círculo por su valor, 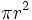 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
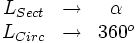
Despejando la longitud del sector:
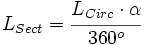
de donde, sustituyendo la longitud de la circunferencia por su valor, 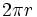 , se obtiene la fórmula.
, se obtiene la fórmula.
|
Actividad interactiva: Sector circular
1. En un círculo de radio 1,80 cm, halla el área de un sector circular de 60º y la longitud de su arco.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Mueve el punto B para modificar el ángulo |
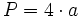
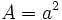

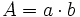
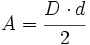

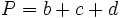
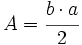
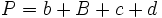
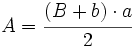
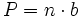
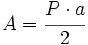
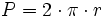
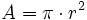
 : número Pi = 3,14159...
: número Pi = 3,14159...
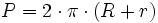
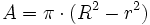
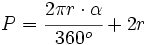
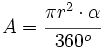
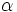 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).

