Medida de la correlación (1ºBach)

De Wikipedia

Menú:
Enlaces internos Para repasar o ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Geogebra
Calculadoras

En el apartado anterior hemos visto de manera intuitiva como puede ser la correlación ente dos variables dependiendo del agrupamiento de los puntos de la nube en torno a una recta. Ahora vamos a ver cómo se puede cuantificar dicha correlación mediante un parámetro que denominaremos coeficiente de correlación.

Dada una distribución bidimensional de cuyas variables 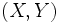\;(X,Y) tenemos 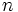\;n valores observados:

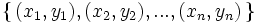
\{ \,(x_1, y_1), (x_2,y_2),...,(x_n,y_n) \,\}

Centro de gravedad de una distribución bidimensional

Llamaremos centro de gravedad de la distribución al punto 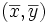(\overline{x} , \overline{y}) cuyas coordenadas son las medias de las distribuciones unidimensionales de X e Y:

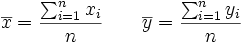
\overline{x}=\frac{\sum_{i=1}^n x_i}{n} \qquad \overline{y}=\frac{\sum_{i=1}^n y_i}{n}

Covarianza

Se llama covarianza de la distribución al parámetro:

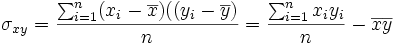
\sigma_{xy}=\frac{\sum_{i=1}^n (x_i-\overline{x})((y_i-\overline{y})}{n}=\frac{\sum_{i=1}^n x_i y_i}{n}-\overline{x} \overline{y}

Correlación

La correlación entre las dos variables viene dada por el parámetro:

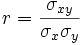
r= \frac{\sigma_{xy}}{\sigma_x \sigma_y}

donde σxy es la covarianza y σx,σy son las desviaciones típicas de las distribuciones unidimensionales de X e Y:

\sigma_x=\sqrt{\frac{\sum_{i=1}^n x_i^2}{n}-\overline{x}^2} \qquad \sigma_y=\sqrt{\frac{\sum_{i=1}^n y_i^2}{n}-\overline{y}^2}

Obtenido de "http://maralboran.org/wikipedia/index.php/Medida_de_la_correlaci%C3%B3n_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda