Pitágoras
De Wikipedia
Pitágoras de Samos (c. 582 - 507 a.C), fue un filósofo y matemático griego. Hombre místico y aristócrata que fundó la Escuela Pitagórica, una especie de secta cuyo símbolo era el pentágono estrellado, y dedicada al estudio de la filosofía, la matemática y la astronomía.
Tabla de contenidos |
Vida
Pitágoras, nació en la isla de Samos en el año 582 a. C. Siendo muy joven viajó a Mesopotamia y Egipto (también, fue enviado por su tío, Zoilo, a Mitilene a estudiar con Ferécides de Syros y tal vez con su padre, Babydos de Syros). Tras regresar a Samos, finalizó sus estudios, según Diógenes Laercio con Hermodamas de Samos y luego fundó su primera escuela durante la tiranía de Polícrates. Abandonó Samos para escapar de la tiranía de Polícrates y se estableció en la Magna Grecia, en Crotona alrededor del 525 a.C., en el sur de Italia, donde fundó su segunda escuela. Las doctrinas de este centro cultural eran regidas por reglas muy estrictas de conducta. Su escuela (aunque rigurosamente esotérica) estaba abierta a hombres y mujeres indistintamente, y la conducta discriminatoria estaba prohibida (excepto impartir conocimiento a los no iniciados). Sus estudiantes pertenecían a todas las razas, religiones, y estratos económicos y sociales. Tras ser expulsados por los pobladores de Crotona, los pitagóricos se exiliaron en Tarento donde se fundó su tercera escuela.
Poco se sabe de la niñez de Pitágoras. Todas las pistas de su aspecto físico probablemente sean ficticias excepto la descripción de una marca de nacimiento llamativa que Pitágoras tenía en el muslo. Es probable que tuviera dos hermanos aunque algunas fuentes dicen que tenía tres. Era ciertamente instruido, aprendió a tocar la lira, a escribir poesía y a recitar a Homero. Había tres filósofos, entre sus profesores, que debieron de haber influido a Pitágoras en su juventud. El esfuerzo para elevarse a la generalidad de un teorema matemático a partir de su cumplimiento en casos particulares ejemplifica el método pitagórico para la purificación y perfección del alma, que enseñaba a conocer el mundo como armonía; en virtud de ésta, el universo era un cosmos, es decir, un conjunto ordenado en el que los cuerpos celestes guardaban una disposición armónica que hacía que sus distancias estuvieran entre sí en proporciones similares a las correspondientes a los intervalos de la octava musical. En un sentido sensible, la armonía era musical; pero su naturaleza inteligible era de tipo numérico, y si todo era armonía, el número resultaba ser la clave de todas las cosas.
La voluntad unitaria de la doctrina pitagórica quedaba plasmada en la relación que establecía entre el orden cósmico y el moral; para los pitagóricos, el hombre era también un verdadero microcosmos en el que el alma aparecía como la armonía del cuerpo. En este sentido, entendían que la medicina tenía la función de restablecer la armonía del individuo cuando ésta se viera perturbada, y, siendo la música instrumento por excelencia para la purificación del alma, la consideraban, por lo mismo, como una medicina para el cuerpo. La santidad predicada por Pitágoras implicaba toda una serie de normas higiénicas basadas en tabúes como la prohibición de consumir animales, que parece haber estado directamente relacionada con la creencia en la transmigración de las almas; se dice que el propio Pitágoras declaró ser hijo de Hermes, y que sus discípulos lo consideraban una encarnación de Apolo.
La escuela pitagórica
A su escuela de pensamiento se la conocía como los pitagóricos y afirmaban que la estructura del universo era aritmética y geométrica. Políticamente apoyaron el partido dórico, obteniendo grandes cuotas de poder hasta el Siglo V, en el que fueron perseguidos y donde muchos de sus miembros murieron. La hermandad estaba dividida en dos partes: Los estudiantes y los oyentes. Los estudiantes aprendían las enseñanzas matemáticas, religiosas y filosóficas directamente de su fundador, mientras que los oyentes se limitaban a ver el modo de comportarse de los pitagóricos.
Pitágoras pasa por ser el introductor de pesos y medidas, y elaborador de la teoría musical (descubrió que las cuerdas de instrumentos musicales producían sonidos de tonos más agudos cuando se las acortaba); el primero en hablar de "teoría" y de "filósofos", en postular el vacío, en canalizar el fervor religioso en fervor intelectual, en usar la definición y en considerar que el universo es una obra sólo descifrable a través de las matemáticas.
Fueron los pitagóricos los primeros en sostener la forma esférica de la tierra y postular que ésta, el sol y el resto de los planetas conocidos, no se encontraban en el centro del universo, sino que giraban en torno a una fuerza simbolizada por el número uno. Ppensaban que todo el universo se apoyaba en los números y sus relaciones, procediendo a revestir a los números de ciertas propiedades mágicas, lo que llevó de una manera indirecta a la investigación sobre las propiedades matemáticas de aquellos.
Primero es la unidad, que cada cosa depende de que sea una, y ese es el principio del uno: que cada algo sea de una cierta manera el todo de si o un punto. Pero lo reiterado ya es otro, no igualdad, sino diferencia que es lo segundo o el dos. El tercero deriva la relación y superficie. El cuatro el tránsito de la superficie a la solidez que representa la pluralidad, la suma de 1, 2, 3 y 4 da 10 (tetraktys), la década, que representa la armonía, cuyo contenido es la progresión lógica que lleva a ella, y desde la cual se reinicia todo movimiento. También se le daba un atributo mágico al número 6, ya que si sumamos o multiplicamos sus divisores (1, 2 y 3) da 6.

Matemáticas
Los pitagóricos atribuían todos sus descubrimientos a Pitágoras por lo que es difícil determinar con exactitud cuales resultados son obra del maestro y cuales de los discípulos.
- Una prueba del teorema de Pitágoras. Si bien los pitagóricos no descubrieron este teorema (ya era conocido y aplicado en Babilonia y la India desde hacía un tiempo considerable), sí fueron los primeros en encontrar una demostración formal del teorema. También demostraron el converso del teorema (si los lados de un triángulo satisfacen la ecuación, entonces el triángulo es recto).
- Ternas pitagóricas. Una terna pitagórica es una terna de números enteros (a, b, c) tales que a²+b²=c². Aunque los babilonios ya sabían cómo generar tales ternas en ciertos casos, los pitagóricos extendieron el estudio del tema encontrando resultados como cualquier entero impar es miembro de una terna pitagórica primitiva. Sin embargo, la solución completa del problema no se obtuvo hasta el siglo XIII cuando Fibonacci encontró la forma de generar todas las ternas pitagóricas posibles.
- Sólidos regulares. Los pitagóricos descubrieron el dodecaedro y demostraron que sólo existen 5 poliedros regulares.
- Números perfectos. Estudiaron los números perfectos, es decir aquellos números que son iguales a la suma de sus divisores propios (por ejemplo 6=1+2+3). Encontraron una fórmula para obtener ciertos números perfectos pares.
- Números amigables. Un par de números son amigables si cada uno es igual a la suma de los divisores propios del otro. Jámblico atribuye a Pitágoras haber descubierto el par amigable (220, 284).
- Números irracionales. El descubrimiento de que la diagonal de un cuadrado de lado 1 no puede expresarse como un cociente de números enteros marca el descubrimiento de los números irracionales.
- Medias. Los pitagóricos estudiaron la relación entre las medias aritmética, geométrica y armónica de dos números y obtuvieron la relación
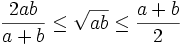 .
.
- Números figurados. Un número es figurado (triangular, cuadrangular, pentagonal, hexagonal, etc) si tal número de guijarros se pueden acomodar formando el polígono correspondiente con lados 1,2,3, etc (ver figura).
El Teorema de Pitágoras
Por muchos años se le ha atribuido a Pitágoras el enunciado y demostración del teorema geométrico que lleva su nombre, el Teorema de Pitágoras. Aunque algunos historiadores consideran lo contrario, ha resultado difícil demostrarlo, debido al misterio que rodeaba las enseñanzas de la escuela, así como el carácter verbal de estas y la obligación de atribuir todos los conocimientos al jerarca de la escuela.
Existen evidencias de que en otras culturas también se conocía el teorema. Por ejemplo, los hindúes explícitamente enuncian una regla equivalente a este teorema en el documento Sulva – Sutra que data del siglo VII A.C. Por otra parte, los Babilonios aplicaban el teorema 2000 años A. C., pero tampoco se conoce de la existencia de una demostración, ya que la geometría no era para ellos una teoría formal sino un cierto tipo de aritmética aplicada, en la cual las figuras venían representadas en forma de números. A su vez, los egipcios conocían que el triángulo de lados 3,4 y 5 es rectángulo pero no se conoce de la existencia de alguna regla que sustente el conocimiento del teorema. Algunos aseguran que durante sus viajes a Egipto y al oriente antiguo, el sabio griego conoció el enunciado de la regla y se dedicó a demostrarla
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz. Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.



