Gauss
De Wikipedia
Johann Carl Friedrich Gauss (1777 – 1855), matemático, astrónomo y físico alemán. Contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Considerado "el príncipe de las matemáticas" y "el matemático más grande desde la antigüedad", Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.
Gauss fue un niño prodigio de quien existen muchas anécdotas acerca de su asombrosa precocidad siendo apenas un infante, e hizo sus primeros grandes descubrimientos mientras era apenas un adolescente. Completó su magnum opus, Disquisitiones Arithmeticae a los veintiún años (1798), aunque no sería publicado hasta 1801. Un trabajo que fue fundamental para que la teoría de los números se consolidara y ha moldeado esta área hasta los días presentes.
Tabla de contenidos |
Vida
Nació el 30 de abril de 1777, en Braunschweig, en el electorado de Brunswick-Lüneburg, que ahora forma parte de la Baja Sajonia, Alemania. Hijo único, de padres de clase trabajadora. Fue bautizado y confirmado en una iglesia cerca de la escuela a la que había asistido de niño. Hay varias historias de su genio precoz. Según una, a la edad de tres años ya dió muestras de sus dones al corregir mentalmente y fallos de cálculo, un error que su padre había cometido en unos cálculos financieros.
Como su padre quería que seguiera sus mismos pasos y se convertiera en albañil, no apoyó la educación de Gauss en matemáticas y ciencias. Gauss recibió apoyo de su madre y del duque de Braunschweig, quien concedió a Gauss una beca para el Colegio Carolinum (ahora Technische Universität Braunschweig), al que asistió entre 1792 y 1795, y posteriormente se trasladó a la Universidad de Göttingen de 1795 a 1798. Si bien en la universidad, independientemente de Gauss redescubrió varios teoremas importantes; [editar] su avance se produjo en 1796 cuando fue capaz de demostrar que cualquier polígono regular con un número de lados que es un primer Fermat (y, por consiguiente, los polígonos con cualquier número de las partes que es el producto de distintos números primos de Fermat y una potencia de 2) puede ser construido por la brújula y escantillón. Este es un importante descubrimiento en un importante campo de las matemáticas, la construcción ha ocupado los problemas matemáticos desde los días de los antiguos griegos, y en última instancia, el descubrimiento condujo a elegir Gauss de matemáticas en lugar de la filología como una carrera. Gauss estaba tan satisfecho por este resultado que pidió que un heptadecagon ser inscrito en su lápida. El albañil disminuido, indicando que la difícil construcción parece esencialmente un círculo [7].
El año 1796 fue muy productivo para ambos Gauss y la teoría de los números. Descubrió una construcción de la heptadecagon el 30 de marzo. [8] Él inventó la aritmética modular, simplificando enormemente las manipulaciones en la teoría de los números. [Editar] Él fue el primero en probar la ley de reciprocidad cuadrática, el 8 de abril. Esta ley muy general permite matemáticos para determinar la solvencia de cualquier ecuación cuadrática en la aritmética modular. El Teorema del número primo, conjectured el 31 de mayo, da una buena comprensión de cómo los números primos se distribuyen entre los enteros. Gauss también descubrió que todo entero positivo es representable como una suma de tres en la mayoría de los números triangulares, el 10 de julio y, a continuación, jotted en su diario las famosas palabras ", Heureka! Num = Δ + Δ + Δ". El 1 de octubre se publicó un resultado sobre el número de soluciones de polinomios con coeficientes en los campos finitos, que en última instancia condujo a la Weil conjeturas 150 años más tarde.
(Por desarrollar)
Gauss murió en Göttingen el 23 de febrero de 1855.
Obra
Infancia
Es célebre la siguiente anécdota: Tenía Gauss diez años cuando un día en la escuela el profesor manda sumar los cien primeros números naturales. El maestro quería unos minutos de tranquilidad... pero transcurridos pocos segundos Gauss levanta la mano y dice tener la solución: los cien primeros números naturales suman 5.050. Y efectivamente es así. ¿Cómo lo hizo Gauss? Pues mentalmente se dio cuenta de que la suma del primer término con el último, la del segundo con el penúltimo, y así sucesivamente, era constante:
Con los 100 números se pueden formar 50 pares, de forma que la solución final viene dada por el producto
Gauss había deducido la fórmula que da la suma de n términos de una progresión aritmética de la que se conocen el primero y el último término:
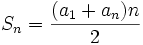
dónde a1 es el primer término, an el último, y n es el número de términos de la progresión.
Juventud
Fue el primero en probar rigurosamente el Teorema Fundamental del Álgebra (disertación para su tesis doctoral en 1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.
En 1801 publicó el libro Disquisitiones Aritmeticae, con seis secciones dedicadas a la Teoría de números, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita del asteroide Cere aproximando parámetros por mínimos cuadrados.
Madurez
En 1809 fue nombrado director del Observatorio de Göttingen. En este mismo año publicó Theoria motus corporum coelestium in sectionibus conicis Solem ambientium describiendo cómo calcular la órbita de un planeta y cómo refinarla posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.
Quizás Gauss haya sido la primera persona en intuir la independencia del postulado de las paralelas de Euclides y de esta manera anticipar una geometría no euclidiana. Pero esto sólo se afirma, sacando conclusiones de cartas enviadas a sus amigos, Farkas Bolyai y a János Bolyai a quien Gauss calificó como un genio de primer orden.
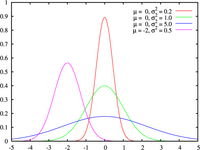
En 1823 publica Theoria combinationis observationum erroribus minimis obnoxiae, dedicado a la estadística, concretamente a la distribución normal cuya curva característica, denominada como Campana de Gauss, es muy usada en disciplinas no matemáticas donde los datos son susceptibles de estar afectados por errores sistemáticos y casuales como por ejemplo la psicología diferencial.
Hay que aclarar que Gauss no fue el primero en hacer referencia a la distribución normal.
Mostró un gran interés en geometría diferencial y su trabajo Disquisitiones generales circa superficies curva publicado en 1828 fue el más reconocido en este campo. En dicha obra expone el famoso teorema egregium. De esta obra se deriva el término curvatura gaussiana.
En 1831 se asocia al físico Wilhelm Weber durante seis fructíferos años en los que realizan investigaciones sobre las Leyes de Kirchhoff, publicaciones sobre magnetismo y construyen un telégrafo eléctrico primitivo.
Aunque a Gauss le desagradaba dar clases, algunos de sus alumnos resultaron destacados matemáticos como Richard Dedekind y Bernhard Riemann. Otros matemáticos contemporáneos fueron Carl Gustav Jakob Jacobi, Dirichlet y Sophie Germain.
Video
Video: Gauss, el príncipe de las matemáticas (22´)
Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo.
Sin embargo la fama de este joven, Gauss le va a venir de los cielos. A finales de 1800 los astrónomos descubren un nuevo objeto celeste. No se trata de un cometa, bien podía ser el planeta buscado tantos años entre Marte y Júpiter. Por desgracia se le pierde la pista. Pero con las pocas observaciones realizadas, Gauss se pone a la tarea de deducir su órbita y señala el lugar del cielo hacia donde apuntar los telescopios un año más tarde. Y en efecto alli aparece Ceres.
Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias.