Funciones: Definición (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Función real de variable real
Una función real de variable real,  , es una correspondencia que a cada número real
, es una correspondencia que a cada número real 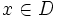 le hace corresponder un único número real
le hace corresponder un único número real  .
.
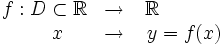
|
Actividades Interactivas: Funciones
1. Determina si son o no son funciones las siguientes gráficas.
Actividad: Una función es una relación entre dos variables numéricas, habitualmente las denominamos  (variable independiente) e (variable independiente) e  (variable dependiente); Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente. (variable dependiente); Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente.
Pero además, para que una relación sea función, a cada valor de la variable independiente le corresponde uno y sólo un valor de la variable dependiente, no le pueden corresponder dos o más valores. a) Observa en la escena las gráficas y di cuál de ellas es función y por qué no lo es la otra. Observa al mover el punto P cuántos puntos de corte tiene la recta azul con cada gráfica; si es más de uno no es una función. |
Dominio de una función
Al conjunto 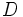 , de los valores que puede tomar la variable independiente
, de los valores que puede tomar la variable independiente  , se le llama dominio de definición de la función. lo representaremos por
, se le llama dominio de definición de la función. lo representaremos por 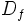 ó
ó 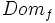
Ejemplo: Dominio de una función
- Halla el dominio de las funciones:
- a)
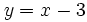 , b)
, b) 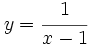 , c)
, c) 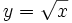
- a)
- a) Su dominio es
 , porque cualquier valor de
, porque cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
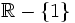 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
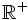 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
(Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos
- Por voluntad de quien propone la función.

