Plantilla:Método de Gauss (1ºBACH)
De Wikipedia
Tabla de contenidos |
Sistema escalonado
Un sistema de ecuaciones se dice que es escalonado si cada ecuación tiene una incógnita más que la siguiente.
Ell siguiente sistema es escalonado:
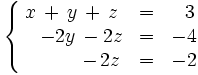
También lo es este otro:
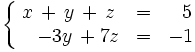
Método reducción de Gauss
El método de Gauss que se debe al matemático alemán Johann Carl Friedrich Gauss, es una generalización del método de reducción, que utilizamos para eliminar una incógnita en los sistemas de dos ecuaciones con dos incógnitas. Consiste en la aplicación sucesiva del método de reducción, utilizando los criterios de equivalencia de sistemas, para transformar el sistema de ecuaciones en un sistema escalonado.
Las operaciones que podemos realizar sobre las ecuaciones del sistema inicial para transformarlo en otro equivalente, son las siguientes:
- Multiplicar o dividir una ecuación por un número real distinto de cero.
- Sumarle o restarle a una ecuación otra ecuación.
- Sumarle a una ecuación otra ecuación multiplicada por un número distinto de cero.
- Cambiar el orden de las ecuaciones.
- Cambiar el orden de las incógnitas del sistema.
- Eliminar ecuaciones nulas (0=0).
Ejemplo: Método de reducción de Gauss
- Resuelve el siguiente sistema de ecuaciones por el método de Gauss:
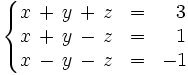
Operamos con las ecuaciones de la siguiente manera:
- Ecu2:
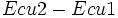
- Ecu3:
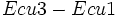
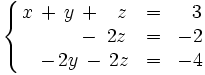
Intercambiamos las dos últimas ecuaciones para dejar el sistema escalonado:
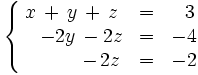
que es equivalente al inicial.
Solucionamos la tercera ecuacion para obtener 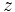 :
:
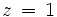
En la primera y segunda ecuación, sustituimos 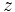 por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación (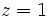 ), para obtener:
), para obtener:
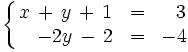
La segunda ecuación es ahora una ecuación con una sola incognita  , que resolvemos para obtener:
, que resolvemos para obtener:
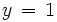
Sustituimos la incógnita  de la primera ecuación, por la solución obtenida en la segunda ecuación (
de la primera ecuación, por la solución obtenida en la segunda ecuación (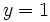 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
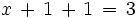
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
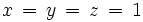
Videotutoriales
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Discusión de sistemas
Después de realizar las transformaciones que se consideren pertinentes, se obtendrá un sistema escalonado. Suponiendo que hubiésemos eliminado, si las hubiera, las filas nulas (0 0 0 ... 0), que corresponden a ecuaciones del tipo 0 = 0, el sistema equivalente tendría ahora k ecuaciones lineales con n incógnitas. Analizando el sistema resultante, podemos efectuar su discusión del siguiente modo:
Sistema incompatible (S.I.)
Si alguna de las ecuaciones es del tipo 0 = b (siendo b distinto de cero), el sistema es incompatible y no tiene solución.
Consideremos el siguiente sistema:
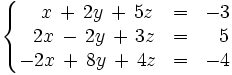
Operamos de la siguiente manera:
- Ecu2:
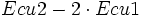
- Ecu3:
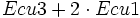
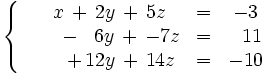
Ahora operamos con la última ecuación para terminar de escalonar:
- Ecu3:
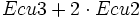
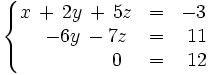
que es equivalente al inicial.
El sistema es incompatible pués la tercera ecuación es absurda.Sistema compatible determinado (S.C.D.)
Si no hay ecuaciones del tipo 0 = b, y además k = n, es decir, el número de ecuaciones del sistema equivalente es igual al número de incógnitas, el sistema es compatible determinado y, por lo tanto, tiene una única solución.
Consideremos el siguiente sistema:
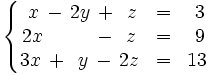
Operamos con las ecuaciones de la siguiente manera:
- Ecu1:
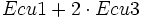
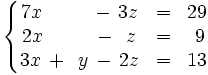
Operamos con las dos primeras ecuaciones para dejar el sistema escalonado
- Ecu1:
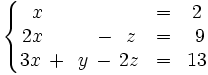
y que es equivalente al inicial.
De la primera ecuacion tenemos el valor de  .
.
En la segunda ecuación, sustituimos  , para obtener
, para obtener 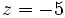
Y, finalmente, en la tercera ecuación sustituimos  y
y 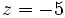 , para hallar
, para hallar 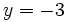 .
.
Así tenemos que la solución del sistema de ecuaciones inicial es:
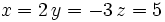
Sistema compatible indeterminado (S.C.I.)
Si no hay ecuaciones del tipo 0 = b y k < n, es decir, el número de ecuaciones es menor que el número de incógnitas, el sistema es compatible indeterminado y, en consecuencia, tiene infinitas soluciones. En este caso, tenemos que separar las incógnitas principales de las no principales. Pero, ¿cuáles son las incógnitas principales? Se puede dar el siguiente criterio: Si el sistema es escalonado y tiene k ecuaciones, las k primeras incógnitas serán las principales y las n - k restantes serán las no principales que pasaremos al segundo miembro como parámetros.
Consideremos el siguiente sistema:
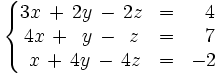
Operamos de la siguiente manera:
- Ecu1:
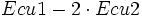
- Ecu3:
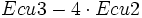
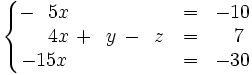
Intercambiamos las dos primeras ecuaciones:
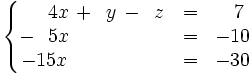
Ahora operamos con las dos últimas ecuaciones:
- Ecu2:
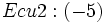
- Ecu3:
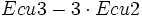
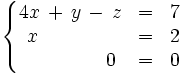
que es equivalente al inicial.
La tercera ecuación se puede suprimir y de la segunda ecuación tenemos que  .
.
Sustituyendo el valor  en la primera ecuación, ésta queda:
en la primera ecuación, ésta queda:
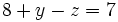
y simplificada:
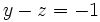
Así nuestro sistema es equivalente a otro con una sola ecuación y dos incógnitas, que por tanto tiene infinitas soluciones, que podemos expresar de la siguiente forma:
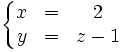
Método de Gauss con matrices
En la siguiente actividad podrás ver como el método de Gauss se puede abreviar utilizando matrices. Estas agilizan el proceso de escalonamiento, ya que, en cada transformación de las ecuaciones del sistema, éstas no se escriben completas sino sólo los coeficientes de las mismas.
|
Actividades Interactivas: Método de Gauss
1. Discusión y resolución de sistemas por el método de Gauss usando matrices.
Actividad: La siguiente escena efectúa la discusión y resuelve, en los casos que proceda (sistema compatible determinado o indeterminado), cualquier sistema de ecuaciones lineales, utilizando el método de Gauss. El número máximo de ecuaciones y de incógnitas que puede tener el sistema es 5. |

