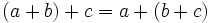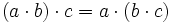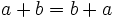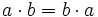Números naturales
De Wikipedia
Tabla de contenidos |
Definición
El conjunto de los números naturales es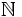 
={0, 1, 2, 3, ...}. Son infinitos y sirven para contar (números cardinales:1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Podemos representarlos en una recta:
Operaciones
Suma y multiplicación
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Resta y división
La resta (o substracción)y la división (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición externa.
Propiedades
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
División
Regla de la división: En toda división, el dividendo es igual al divisor por el cociente más el resto.
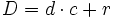
Potenciación
Actividades Interactivas - Potencia de exponente natural
