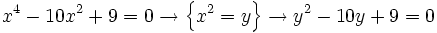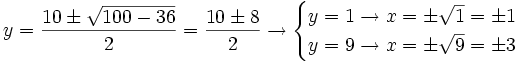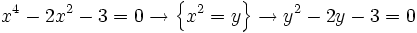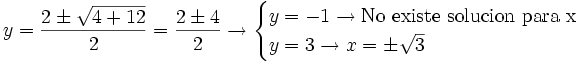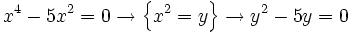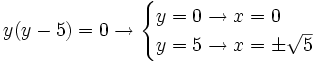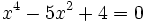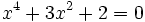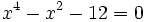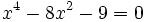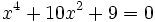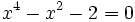Plantilla:Ecuaciones bicuadradas
De Wikipedia
Las ecuaciones bicuadradas Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma
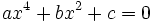
El truco para resolverlas es hacer el cambio de variable 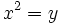 . Entonces, la ecuación quedará como una de segundo grado
. Entonces, la ecuación quedará como una de segundo grado
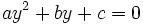
Una vez resuelta esta ecuación en  , tenemos que averiguar el valor de la
, tenemos que averiguar el valor de la  . Para ello desharemos el cambio de variable, haciendo
. Para ello desharemos el cambio de variable, haciendo 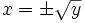 . En consecuencia, las soluciones
. En consecuencia, las soluciones 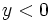 , las rechazaremos, ya que no darán solución para la
, las rechazaremos, ya que no darán solución para la 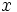 , quedándonos sólo con las soluciones de
, quedándonos sólo con las soluciones de 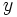 no negativas, cada una de las cuales dará dos soluciones para la
no negativas, cada una de las cuales dará dos soluciones para la 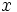 .
.
Ejercicios resueltos: Ecuaciones bicuadradas
- Resuelve las ecuaciones:
- a)
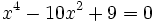
- a)
- b)
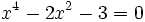
- b)
- c)
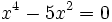
- c)
a)
- Soluciones:
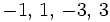
b)
- Soluciones:
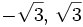
c)
- Soluciones:
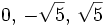
Videotutoriales
- Método de resolución de ecuaciones bicuadradas.
- Ejemplos.
Resolución de las siguientes ecuaciones:
- a) x4 + 3x2 − 4 = 0
- b) x4 − 9x2 = 0
- c) x4 − 9 = 0
- d) x4 + 5 = 0
- e) x6 − 9x3 + 8 = 0
|
Actividad: Ecuaciones bicuadradas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
(pág. 75)
|
Ejercicios propuestos: Ecuaciones bicuadradas |