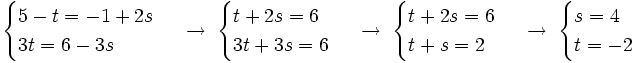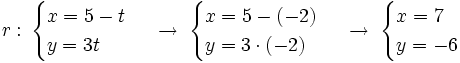Posiciones relativas de dos rectas del plano (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 200)
Posición relativa de dos rectas en el plano
Dadas las ecuaciones de dos rectas del plano, éstas pueden ser secantes, paralelas o coincidentes.
Veamos como se averigua dependiendo del tipo de ecuaciones que nos den.
Posición relativa de dos rectas dadas en ecuaciones paramétricas
Procedimiento
Dadas las rectas: 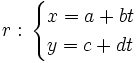 y
y 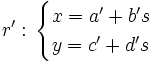
para hallar su posición relativa igualaremos las incógnitas y resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas, 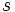 y
y 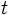 :
:
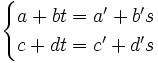
- Si el sistema es compatible determinado (una solución:
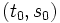 ), las dos rectas se cortan en un punto, que se obtiene sustituyendo los parámetros
), las dos rectas se cortan en un punto, que se obtiene sustituyendo los parámetros 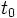 y
y 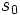 , en las ecuaciones paramétricas.
, en las ecuaciones paramétricas.
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas.
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes.
Ejemplo: Posición relativa de dos rectas
Determina la posición relativa de las rectas: 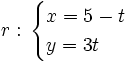 y
y 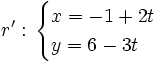
Hay que cambiar el parámetro "t" en una de las dos ecuaciones (por ejemplo la segunda) por otro distinto "s".
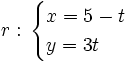 ;
; 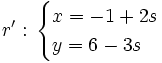
A continuación se resuelve el siguiente sistema:
Luego las rectas son secantes, y su punto de corte lo obtenemos sustituyendo estas soluciones en cualquiera de las dos ecuaciones paramétricas, por ejemplo, en la primera:
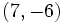 .
.Posición relativa de dos rectas dadas en ecuaciones implícitas
Procedimiento
Dadas las rectas: 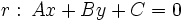 y
y 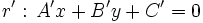
para hallar su posición relativa resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas:, 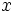 e
e 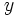 :
:
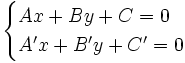
- Si el sistema es compatible determinado (una solución:
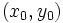 ), las dos rectas se cortan en ese punto. (Esto ocurre cuando
), las dos rectas se cortan en ese punto. (Esto ocurre cuando 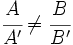 ).
).
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas. (Esto ocurre cuando
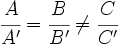 ).
).
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes. (Esto ocurre cuando
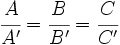 ).
).
Ejemplo: Posición relativa de dos rectas
Determina la posición relativa de las rectas: 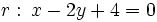 y
y 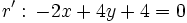
Hay que resolver el siguiente sistema.
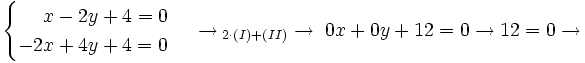 No tiene solución.
No tiene solución.
En esta escena podrás ver las distintas posiciones relativas de dos rectas en el plano.
Posición relativa de dos rectas dadas en ecuaciones explícitas
Procedimiento
Dadas las rectas: 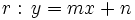 y
y 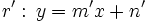
para hallar su posición relativa resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas:, 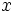 e
e 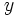 :
:
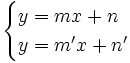
- Si el sistema es compatible determinado (una solución:
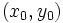 ), las dos rectas se cortan en ese punto. (Esto ocurre cuando las pendientes son distintas:
), las dos rectas se cortan en ese punto. (Esto ocurre cuando las pendientes son distintas: 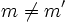 ).
).
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas. (Esto ocurre cuando
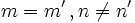 ).
).
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes. (Esto ocurre cuando
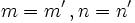 ).
).
Videotutoriales
Sean las rectas A1.x + B1.y + C1 = 0 y A2.x + B2.y + C2 = 0.
- Si A1/A2 = B1/B2 = C1/C2, las rectas son la misma.
- Si A1/A2 = B1/B2 pero no coincide con C1/C2, las rectas son paralelas.
- En otros casos las rectas se cortan en el punto cuyas coordenadas corresponden a la única solución que tiene el sistema que forman las ecuaciones de las rectas.
En los dos problemas de este vídeo nos dan dos rectas y una de ellas tiene coeficientes "locos". Debemos determinar esos coeficientes locos para que las rectas tengan una posición relativa concreta.
Debemos demostrar que cuatro rectas dadas forman un paralelogramo (son paralelas dos a dos) y determinar su centro.
Ejercicios propuestos
|
Ejercicios propuestos: Posición relativa de dos rectas en el plano |