Ecuaciones de primer grado (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 106)
Ecuación de primer grado
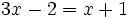 (Ecuación de primer grado con una incógnita)
(Ecuación de primer grado con una incógnita)
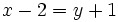 (Ecuación de primer grado con dos incógnitas)
(Ecuación de primer grado con dos incógnitas)
 (No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2)
(No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2)
Nota: Una ecuación de primer grado puede no parecerlo antes de reducirla. Será necesario operar y transponer términos antes de poder determinar el tipo de ecuación. Por ejemplo, la ecuación puede tener algunos monomios de grado 2 o superior pero conseguir que éstos desaparezcan tras reducirla, quedando sólo términos de grado 1.
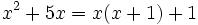 parece de segundo grado, pero al reducirla queda
parece de segundo grado, pero al reducirla queda 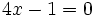 que es de primer grado.
que es de primer grado.
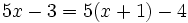 parece de primer grado, pero al reducirla queda
parece de primer grado, pero al reducirla queda 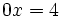 , o bien,
, o bien, 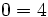 , que es de grado cero.
, que es de grado cero.
Ecuación de primer grado con una incógnita
Solución de la ecuación de primer grado con una incógnita
Toda ecuación de primer grado con una incógnita se puede reducir a la forma:
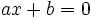
con 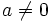 , cuya única solución es:
, cuya única solución es:
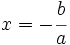
Nota: Si al reducir la ecuación de partida resulta que el coeficiente de primer grado es 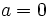 , entonces la ecuación de partida no es realmente de primer grado, sino de grado cero. Estos caso especiales los estudiaremos en otro apartado de este tema.
, entonces la ecuación de partida no es realmente de primer grado, sino de grado cero. Estos caso especiales los estudiaremos en otro apartado de este tema.
En la siguiente escena tienes ejemplos de soluciones de ecuaciones de primer grado con una incógnita.
Pulsa los botones para ver más ecuaciones.
Actividades en la que aprenderás a resolver ecuaciones de primer grado con una incógnita sencillas.
Ecuaciones equivalentes
Dos ecuaciones son equivalentes si tienen las mismas soluciones.
Transformaciones que mantienen la equivalencia de las ecuaciones
A partir de una ecuación podemos obtener otra equivalente si efectuamos alguna de las siguientes operaciones:
- Regla de la suma: Sumar o restar la misma expresión en los dos miembros de la igualdad. (Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.)
- Regla del producto: Multiplicar o dividir los dos miembros de la igualdad por un mismo número distinto de cero. (Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.)
Tutorial en el que se muestra como expresar cualquier ecuación en su forma general o canónica. El proceso requerirá del uso de la regla de la suma y del producto para obtener ecuaciones equivalentes cada vez más sencillas.
Ejercicios de autoevaluación sobre ecuaciones equivalentes.
Resolución de ecuaciones de primer grado
Procedimiento
Para resolver una ecuación de primer grado hay que transformarla en otras ecuaciones equivalentes, cada vez más sencillas, hasta conseguir despejar la incógnita.
Los pasos que hay que dar pueden ser los siguientes, aunque algunos pueden variar de orden según los casos:
- Quitar denominadores, si los hay (multiplicando los dos miembros de la ecuación por el mínimo común múltiplo de los denominadores).
- Quitar paréntesis, si los hay.
- Transponer términos, pasando las incógnitas a un lado y los números al otro (Usaremos la primera de las transformaciones descritas en el apartado anterior)
- Simplificar cada miembro (agrupando términos numéricos y términos con incógnita) hasta obtener una expresión del tipo
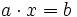 .
.
- Despejar la incógnita, x, obteniendo la solución (Usaremos la segunda de las transformaciones descritas en el apartado anterior, siempre que
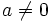 . (Si fuese
. (Si fuese 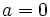 , estaríamos un caso especial que se analizará en el apartado de "casos especiales".)
, estaríamos un caso especial que se analizará en el apartado de "casos especiales".)
- Podemos, opcionalmente, comprobar la solución. Para ello sustituiremos la incógnita por la solución en los dos miembros de la ecuación de partida y los resultados deben coincidir.
Casos especiales
Tras efectuar el procedimiento anterior, si en la expresión 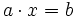 del paso 4º, resultase que el coeficiente de la variable
del paso 4º, resultase que el coeficiente de la variable  es cero, tendríamos:
es cero, tendríamos:
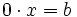
Entonces, al no poder dividir por 0 para despejar la  (paso 5º), llegaríamos a uno de los siguientes dos casos especiales:
(paso 5º), llegaríamos a uno de los siguientes dos casos especiales:
Casos especiales
-
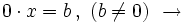 La ecuación no tiene solución.
La ecuación no tiene solución.
-
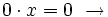 La ecuación tiene infinitas soluciones.
La ecuación tiene infinitas soluciones.
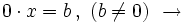 Si
Si 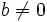 , como el miembro de la izquierda es siempre igual a cero, sea cual sea el valor de
, como el miembro de la izquierda es siempre igual a cero, sea cual sea el valor de  , la igualdad es imposible. Por tanto no hay solución.
, la igualdad es imposible. Por tanto no hay solución.
-
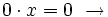 El miembro de la izquierda es siempre igual a cero, por tanto, sea cual sea el valor de
El miembro de la izquierda es siempre igual a cero, por tanto, sea cual sea el valor de  , la igualdad se cumple. Luego, cualquier número es solución de la ecuación.
, la igualdad se cumple. Luego, cualquier número es solución de la ecuación.
-
 No tiene solución, ya que no hay ningún número que multiplicado por 0 de 7.
No tiene solución, ya que no hay ningún número que multiplicado por 0 de 7.
-
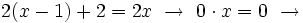 La ecuación tiene infinitas soluciones, ya que cualquier número multiplicado por 0 da 0.
La ecuación tiene infinitas soluciones, ya que cualquier número multiplicado por 0 da 0.
Resuelve:
- a)

- b)
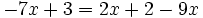
- c)
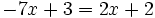
Resuelve:
Completa la ecuación para que no tenga solución:
- 7x - 9 = ___ x + ___
Completa la ecuación para que tenga infinitas soluciones:
- 4(x - 2) + x = 5x + ___
Número de soluciones de una ecuación de primer grado.
Número de soluciones de una ecuación de primer grado.
Actividades
Resuelve: ![15x-[8x-(2-10x)]=24x+[-(3x+7)-(x+1)]\;](/wikipedia/images/math/3/c/1/3c19d21c3f8ae649f07ab28578e41c8d.png)
Resuelve: 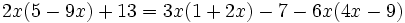
Resuelve: 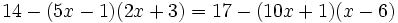
Resuelve: 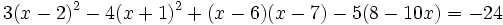
Resuelve: 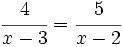
Resuelve:
a) 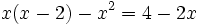
b) 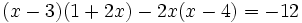
Resuelve:
a) 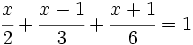
b) 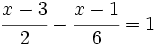
c) 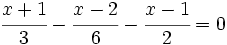
Resuelve:
a) 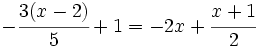
b) 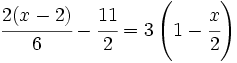
Resuelve:
a) 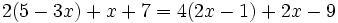
b) 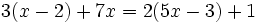
Resuelve:
a) 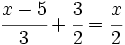
b) 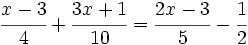
Despeja x en la siguiente ecuación con coeficientes desconocidos:
Actividades en la que aprenderás a resolver ecuaciones de primer grado más complejas.
Ejercicios de autoevaluación sobre resolución de ecuaciones de primer grado.
Autoevaluación sobre ecuaciones de primer grado.
Ecuaciones de primer grado con coeficientes desconocidos.
Ejercicios resueltos sobre ecuaciones de primer grado.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones de primer grado |
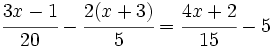
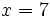
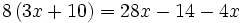
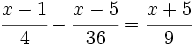
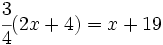
![ax+3x=bx]5\;](/wikipedia/images/math/2/e/4/2e4f350fe4c8504518250c11f80dc17b.png)

