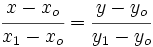Plantilla:Ecuación de la recta que pasa por dos puntos
De Wikipedia
Dos puntos determinan una única recta que pasa por ellos. Veamos como se obtiene su ecuación:
Procedimiento
Sean 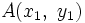 y
y 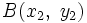 dos puntos de una recta. Para hallar su ecuación procederemos como sigue:
dos puntos de una recta. Para hallar su ecuación procederemos como sigue:
- Con los dos punto hallaremos la pendiente:
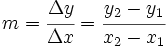
- A continuación podemos seguir dos caminos:
- a) Usar la ecuación punto-pendiente: con uno cualquiera de los dos puntos y con la pendiente que acabamos de calcular.
- b) Usar la ecuación explícita,
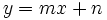 : sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de
: sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de  .
.
Ejemplo: Ecuación de la recta que pasa por dos puntos
Halla la ecuación de la recta que pasa por los puntos (2, 4) y (-3, 5).
Solución:
Hallamos la pendiente:

- Primer método: Usando la ecuación punto-pendiente con el punto (2,4) y la pendiente


- Segundo método: Usando la ecuación explícita con el punto (2,4) y la pendiente

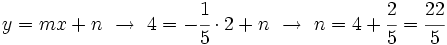
- de donde:
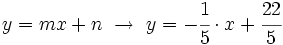
|
Actividades Interactivas: Ecuación de la recta que pasa por dos puntos
1. Ecuación punto-pendiente de la recta que pasa por dos puntos.
Actividad: Por dos puntos distintos pasa una única recta. Si los puntos son 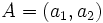 y y 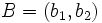 la ecuación de la recta que pasa por ellos es: la ecuación de la recta que pasa por ellos es:
con a) Calcula la ecuación de la recta que pasa por los puntos (2,-3) y (5, 4) y compruébala en la siguiente escena:
2. Ecuaciones continua y general de la recta que pasa por dos puntos.
Actividad: La ecuación continua de la recta que pasa por los puntos 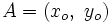 y y 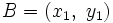 es: es:
a) Calcula la ecuación continua y general de la recta que pasa por los puntos (-1,3) y (1, 2) y compruébala en la siguiente escena: b) Comprueba si los puntos A(1,0), B(2,1) y C(3,3) están o no alineados. (Sugerencia: Calcula la recta que pasa por A y B, y comprueba que C pertenece a ella.) |
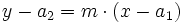
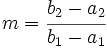 .
.