Plantilla:Ecuación de la recta que pasa por dos puntos
De Wikipedia
Dos puntos determinan una única recta que pasa por ellos. Veamos como se obtiene su ecuación:
Procedimiento
Sean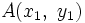 
y 
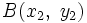dos puntos de una recta. Para hallar su ecuación procederemos como sigue:
- Con los dos punto hallaremos la pendiente:
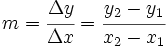
- A continuación podemos seguir dos caminos:
- a) Usar la ecuación punto-pendiente: con uno cualquiera de los dos puntos y con la pendiente que acabamos de calcular.
- b) Usar la ecuación explícita,
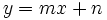: sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de 
.
En esta escena podrás ver practicar el cálculo de la ecuación de la recta que pasa por dos puntos dados.
Ejercicio 1 (4'51") Sinopsis: Determina la ecuación general de la recta que pasa por los puntos (3,2) y (-1,-2).
Ejercicio 2 (4'57") Sinopsis: Si una recta pasa por los puntos (-2,-6) y (-5,p), y tiene pendiente -9/4, hallar el valor de "p".
Ejercicio 3 (3'26") Sinopsis: Determina la ecuación explícita de la recta que tiene abscisa al origen 3 y ordenada al origen 5.
