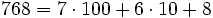Sistemas de numeración (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 8)
Sistemas de numeración
| Los números surgen de la necesidad de contar. Por ejemplo, el hombre primitivo, para contar los animales de su rebaño, hacia uso de semillas o guijarros; muescas en palos, huesos o piedras; etc.
En numerosas civilizaciones el hombre uso su cuerpo, dándole a sus partes (manos, pies, falanges, ...) valores numéricos. A medida que la sociedad fue evolucionando, surgió la necesidad de contar cantidades más grandes, para lo que hubo que inventar nuevos símbolos. Los símbolos utilizados para representar los números y sus normas de uso forman un sistema de numeración. |
Una mirada humorística a los primeros intentos de crear sistemas de numeración, que conducen a nuestro moderno sistema decimal de base 10, el cual hace uso de la "notación posicional". La historia transcurre en la ficticia isla de Cocoloco.
Tipos de sistemas de numeración
Podemos distinguir dos tipos de sistemas de numeración: aditivos y posicionales.
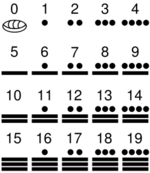
Algunos sistemas de numeración son mixtos, es decir, tienen algo de aditivos y algo de posicionales. (Ej. sist. num. romano y maya). Tutorial que muestra una breve introducción a los sistemas de numeración: aditivos, multiplicativos y posicionales. Explicación de algunos de los más importantes sistemas de numeración a lo largo de la historia, del egipcio hasta el binario, pasando por el griego, maya, chino, hindú... - 00:00 a 01:30: Introducción. - 01:30 a 03:41: Sistema Egipcio. Sistema Aditivo. - 03:41 a 07:40: Sistema Babilónico. Sistema Posicional. - 07:40 a 10:10: Sistema Griego. Sistema Aditivo. - 10:10 a 12:10: Sistema Chino. Sistema Multiplicativo. - 12:10 a 16:00: Sistema Maya. Sistema Posicional. - 16:00 a 17:10: Sistema Romano. Sistema Aditivo. - 17:10 a 22:20: Sistema Hindú. Sistema Posicional. + 18:45 : Sistema Decimal. - 22:20 a 25:42: Sistemas de Numeración en la Informática (Binario, Octal, Hexadecimal). Tutorial que explica a fondo el sistema de numeración binario, tanto su fundamento como su paso al sistema decimal y viceversa. También da algunas pinceladas del sistema hexadecimal y octal. ¿Para qué sirven los números romanos? ¿Cuáles son los números romanos? ¿Y sus reglas? ¿Cuál es su origen? Descubre los números romanos y aprende a escribir como lo hicieron nuestros antepasados. Sistema de numeración romano. Reglas. Cómo pasar del sistema de numeración romano al decimal y del sistema decimal al romano. Ejemplos. Números romanos son un sistema antiguo de numeración decimal. La comprensión de las cifras romanas (con notación aditiva) puede arrojar luz sobre nuestro moderno sistema de numeración que emplea notación posicional. Our modern decimal number system is base-10. Other number systems used in fields like computer engineering are base-2 (binary), base-8 (octal) and base-16 (hexadecimal). (Disponibles los subtítulos en inglés) |
Exposición interactiva para repasar el sistema de numeración romano
|
Actividad: Sistemas de numeración
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
El sistema de numeración decimal
Es nuestro sistema de numeración, nacido en la India en el siglo V y que llegó a Europa por medio de los árabes.
- El sistema de numeración decimal es un sistema de numeración posicional que utiliza 10 símbolos o cifras: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9.
- Al ser un sistema de numeración posicional cada cifra, dependiendo del lugar que ocupe, tiene un valor. Así tenemos diferentes órdenes o categorías de unidades: unidades, decenas, centenas,...
- En este sistema, diez unidades de un orden cualquiera hacen una unidad del orden inmediato superior:
- 1 decena = 10 unidades
- 1 centena = 10 decenas = 100 unidades
- 1 unidad de millar = 10 centenas = 1000 unidades
- 1 decena de millar = 10 unidades de millar = 10,000 unidades
- 1 centena de millar = 10 decenas de millar = 100,000 unidades
- 1 unidad de millón = 10 centenas de millar = 1,000,000 unidades
- 1 decena de millón = 10 unidades de millón = 10,000,000 unidades
- etc.
El número:
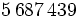
Se lee:
Las cifras ocupan los siguientes órdenes de unidades:
unid. millón |
cent. millar |
dec. millar |
unid. millar |
centenas |
decenas |
unidades |
5 |
6 |
8 |
7 |
4 |
3 |
9 |
5,000,000 unid. |
600,000 unid. |
80,000 unid. |
7,000 unid. |
400 unid. |
30 unid. |
9 unid. |
Aprende a manejar la tabla de valor posicional para identificar las distintas unidades de un número
El sistema de numeración decimal permite escribir cualquier número con diez símbolos:
Estos diez símbolos se llaman cifras o dígitos.
En un número, el valor de cada cifra depende de la posición que ocupa: unidades, decenas, centenas, unidades de mil o de millar, decenas de millar...
Esta actividad consiste en arrastrar un círculo hasta la unidad que se te indica.
Lectura y escritura de números naturales
Reglas
- Al leer números, primero se separan las cifras de tres en tres empezando por la derecha. Después se leen de izquierda a derecha como si fuesen números de tres cifras y se añaden las palabras mil, millones, billones, trillones,... donde corresponda.
- Hasta el número treinta siempre se escribe con una sola palabra.
- Según indica la Real Academia Española al escribir números de más de cuatro cifras, se agruparán estas de tres en tres, empezando por la derecha, y separando los grupos por espacios en blanco:
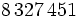 (y no por puntos o comas). Los números de cuatro cifras se escriben sin espacios de separación: 2458.
(y no por puntos o comas). Los números de cuatro cifras se escriben sin espacios de separación: 2458.
Notación desarrollada de un número
La notación desarrollada de un número consiste en expresarlo como suma de los valores relativos de cada uno de sus dígitos.
Escribe en notación desarrollada los números:
a) 385
b) 1834
Escribe en notación desarrollada los números:
a) 672
b) 4521
Escribe en notación desarrollada los números:
a) 23772
b) 127050
Ejercicios propuestos
|
Ejercicios propuestos: Sistemas de numeración |