Simetrías (1º ESO)
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
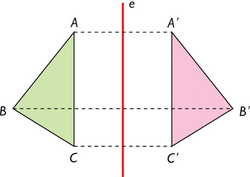
Simetría axial
Procedimiento Dado un punto A, para obtener su simétrico, A', respecto de una recta "e", se siguen los siguientes pasos:
La simetría axial. Ejemplos. En este vídeo trazamos la simetría axial de un polígono.
|
Proposición
Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes contiguos forman un ángulo de 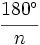 .
.