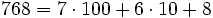Sistemas de numeración (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
(Pág. 8)
Introducción
- Sabrías sumar de forma fácil y sin calculadora los 100 primeros números naturales?
- El misterioso número 6174.
Sistemas de numeración
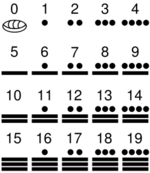
| Los números surgen de la necesidad de contar. Por ejemplo, el hombre primitivo, para contar los animales de su rebaño, hacia uso de semillas o guijarros; muescas en palos, huesos o piedras; etc.
En numerosas civilizaciones el hombre uso su cuerpo, dándole a sus partes (manos, pies, falanges, ...) valores numéricos. A medida que la sociedad fue evolucionando, surgió la necesidad de contar cantidades más grandes, para lo que hubo que inventar nuevos símbolos. Los símbolos utilizados para representar los números y sus normas de uso forman un sistema de numeración. |
Una mirada humorística a los primeros intentos de crear sistemas de numeración, que conducen a nuestro moderno sistema decimal de base 10, el cual hace uso de la "notación posicional". La historia transcurre en la ficticia isla de Cocoloco.
Tipos de sistemas de numeración
Podemos distinguir dos tipos de sistemas de numeración: aditivos y posicionales.
Algunos sistemas de numeración son mixtos, es decir, tienen algo de aditivos y algo de posicionales. (Ej. sist. num. romano y maya). Tutorial que muestra una breve introducción a los sistemas de numeración: aditivos, multiplicativos y posicionales. Explicación de algunos de los más importantes sistemas de numeración a lo largo de la historia, del egipcio hasta el binario, pasando por el griego, maya, chino, hindú... - 00:00 a 01:30: Introducción. - 01:30 a 03:41: Sistema Egipcio. Sistema Aditivo. - 03:41 a 07:40: Sistema Babilónico. Sistema Posicional. - 07:40 a 10:10: Sistema Griego. Sistema Aditivo. - 10:10 a 12:10: Sistema Chino. Sistema Multiplicativo. - 12:10 a 16:00: Sistema Maya. Sistema Posicional. - 16:00 a 17:10: Sistema Romano. Sistema Aditivo. - 17:10 a 22:20: Sistema Hindú. Sistema Posicional. + 18:45 : Sistema Decimal. - 22:20 a 25:42: Sistemas de Numeración en la Informática (Binario, Octal, Hexadecimal). Tutorial que explica a fondo el sistema de numeración binario, tanto su fundamento como su paso al sistema decimal y viceversa. También da algunas pinceladas del sistema hexadecimal y octal. ¿Para qué sirven los números romanos? ¿Cuáles son los números romanos? ¿Y sus reglas? ¿Cuál es su origen? Descubre los números romanos y aprende a escribir como lo hicieron nuestros antepasados. Sistema de numeración romano. Reglas. Cómo pasar del sistema de numeración romano al decimal y del sistema decimal al romano. Ejemplos. Números romanos son un sistema antiguo de numeración decimal. La comprensión de las cifras romanas (con notación aditiva) puede arrojar luz sobre nuestro moderno sistema de numeración que emplea notación posicional. Our modern decimal number system is base-10. Other number systems used in fields like computer engineering are base-2 (binary), base-8 (octal) and base-16 (hexadecimal). (Disponibles los subtítulos en inglés) |
|
Actividad: Sistemas de numeración
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
El sistema de numeración decimal
Es nuestro sistema de numeración, nacido en la India en el siglo V y que llegó a Europa por medio de los árabes.
- El sistema de numeración decimal es un sistema de numeración posicional que utiliza 10 símbolos o cifras: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9.
- Al ser un sistema de numeración posicional cada cifra, dependiendo del lugar que ocupe, tiene un valor. Así tenemos diferentes órdenes o categorías de unidades: unidades, decenas, centenas,...
- En este sistema, diez unidades de un orden cualquiera hacen una unidad del orden inmediato superior:
- 1 decena = 10 unidades
- 1 centena = 10 decenas = 100 unidades
- 1 unidad de millar = 10 centenas = 1000 unidades
- 1 decena de millar = 10 unidades de millar = 10,000 unidades
- 1 centena de millar = 10 decenas de millar = 100,000 unidades
- 1 unidad de millón = 10 centenas de millar = 1,000,000 unidades
- 1 decena de millón = 10 unidades de millón = 10,000,000 unidades
- etc.
El número:
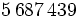
Se lee:
Las cifras ocupan los siguientes órdenes de unidades:
unid. millón |
cent. millar |
dec. millar |
unid. millar |
centenas |
decenas |
unidades |
5 |
6 |
8 |
7 |
4 |
3 |
9 |
5,000,000 unid. |
600,000 unid. |
80,000 unid. |
7,000 unid. |
400 unid. |
30 unid. |
9 unid. |
Practica con el valor posicional de las cifras de un número.
Aprende a manejar la tabla de valor posicional para identificar las distintas unidades de un número
Los números naturales
El conjunto de los números naturales es:
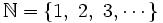
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Representación de los números naturales
Representación de los números naturales
Orden en los números naturales
En la representación de los números naturales en la recta numérica se observa la relación de orden que existe en dicho conjunto. Diremos que los números naturales están ordenados (véase números ordinales), lo que nos permite comparar dos números naturales entre sí.
Un número natural es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Orden en el conjunto de los números naturales
Dados dos números naturales cualesquiera,  y
y  , se dará uno de los siguientes casos:
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
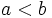 (Se lee "a es menor que b").
(Se lee "a es menor que b").
- El primero es igual que el segundo:
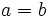 (Se lee "a es igual que b").
(Se lee "a es igual que b").
- El primero es mayor que el segundo:
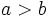 (Se lee "a es mayor que b").
(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
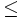 )
)
- Mayor o igual que (
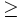 )
)
- Distinto (
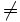 )
)
Comparación de números naturales.
Orden y comparación de números naturales.
Igualdad y desigualdad de números naturales. Simbología. Ejemplos.
Completa el hueco con el signo "mayor que" (>), "menor que" (<) o "igual" (=):
- siete millares + nueve centenas + siete unidades ___ 7000 + 970
¿Cuál es el menor número con 5 cifras? (los ceros a la izquierda no cuentan)
¿Cuál es el mayor número de 6 cifras?
Escribe el mayor número posible con las cifras 3, 5, 2, 8, 9 y 6.
Compara números de 2 dígitos.
Notación desarrollada de un número natural
La notación desarrollada de un número natural consiste en expresarlo como suma de los valores relativos de cada uno de sus dígitos.
Notación desarrollada de números naturales.
Notación desarrollada.
Ejemplos de notación desarrollada de un número natural
Escribe en notación desarrollada los números:
a) 385
b) 1834
Escribe en notación desarrollada los números:
a) 672
b) 4521
Escribe en notación desarrollada los números:
a) 23 772
b) 127 050
Escribe en notación desarrollada el número 14 897.
Lectura y escritura de números naturales
Reglas
- Al leer números, primero se separan las cifras, de tres en tres, empezando por la derecha. Después se leen de izquierda a derecha, como si fuesen números de tres cifras, y se añaden las palabras mil, millones, billones, trillones,... donde corresponda.
- Hasta el número treinta siempre se escribe con una sola palabra.
- Según indica la Real Academia Española, al escribir números de más de cuatro cifras, se agruparán estas de tres en tres, empezando por la derecha, y separando los grupos por espacios en blanco y no por puntos o comas (8 327 451). Los números de cuatro cifras se escriben sin espacios de separación (2458).
Lectura y escritura de números naturales
Escribe cómo se lee el número 3 454 783 215 571 247 869 523
Escribe cómo se leen los números:
- a) 12 529 345 897 883 143
- b) 1 450 937 845 967 388 492 123
Escribe el número "seiscientos cuarenta y cinco millones, quinientos ochenta y cuatro mil, cuatrocientos sesenta y dos".
Practica la lectura y escritura de números naturales.
Autoevaluación sobre lectura y escritura de números naturales y sobre cómo expresarlos en forma desarrollada.
Los números grandes
Los números naturales son infinitos y nuestro sistema de numeración decimal nos permite representar cualquiera de ellos por muy grandes que sean.
Los números grandes más usuales son:
- 1 millón = 1 000 000 (1 seguido de 6 ceros)
- 1 billón = 1 millón de millones = 1 000 000 000 000 (1 seguido de 12 ceros)
- 1 trillón = 1 millón de billones = 1 000 000 000 000 000 000 (1 seguido de 18 ceros)
- 1 millardo = Mil millones = 1 000 000 000 (1 seguido de 9 ceros)
Exposición interactiva de la representación de números grandes en el sistema de numeración decimal.
Desde el millón hasta el quintillón.
¿Hasta qué número es posible contar? ¿Hay un número mayor que todos, o la cuenta no acaba nunca y es infinita? ¿Cuál es el número más grande que alguien haya podido imaginar? Errata en minuto 1:05 -> en realidad ese número se lee "setenta mil trillones" en español y en inglés si sería "seventy sextillion" por lo que hay un error en el vídeo.
Aunque parezca que los grandes números son muy modernos, no es así en absoluto. En la Universidad de Oxford se conserva una pieza egipcia de unos 5000 años de antigüedad que registra la victoria del rey Narmer sobre los libaneses al oeste del delta del Nilo; en ella se describe que Egipto se cobró 120 000 prisioneros, 400 000 bueyes y 1 422 000 cabras. Los centenares de miles y los millones también se hallan mencionados en el egipcio "Libro de los muertos".
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 12)"
El conjunto de los números naturales es:
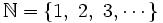
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Representación de los números naturales
Podemos representarlos en una recta. Sobre ella marcamos el número cero. A la derecha del cero, y con las mismas separaciones, situamos de menor a mayor los siguientes números naturales: 1, 2, 3,...
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Lectura y escritura de números naturales
Reglas
- Al leer números, primero se separan las cifras de tres en tres empezando por la derecha. Después se leen de izquierda a derecha como si fuesen números de tres cifras y se añaden las palabras mil, millones, billones, trillones,... donde corresponda.
- Hasta el número treinta siempre se escribe con una sola palabra.
- Según indica la Real Academia Española al escribir números de más de cuatro cifras, se agruparán estas de tres en tres, empezando por la derecha, y separando los grupos por espacios en blanco: 8 327 451 (y no por puntos o comas). Los números de cuatro cifras se escriben sin espacios de separación: 2458.
Practica la lectura y escritura de números naturales.
Notación desarrollada de un número natural
La notación desarrollada de un número natural consiste en expresarlo como suma de los valores relativos de cada uno de sus dígitos.
Escribe en notación desarrollada los números:
a) 385
b) 1834
Escribe en notación desarrollada los números:
a) 672
b) 4521
Escribe en notación desarrollada los números:
a) 23772
b) 127050
Ejercicios propuestos
|
Ejercicios propuestos: Sistemas de numeración |