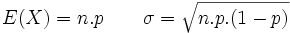La distribución binomial
De Wikipedia
Distribución binomial
Supongamos que un experimento aleatorio tiene las siguientes caracteristicas:
|
|
Todo experimento aleatorio con estas características se dice que sigue el modelo de la distribución binomial. Su función de probabilidad queda determinada por n número de pruebas idénticas realizadas y p probabilidad de éxito en una de ellas.
A la variable X , que representa el número de éxitos obtenidos en el experimento, se le llama variable aleatoria binomial B(n,p).
Su función de probabilidad es:
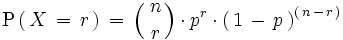
|
Además
|
|
Obtención de la función de probabilidad.
Existen varias maneras de obtener
r
exitos en las
n
pruebas. Supongamos que lanzamos una moneda
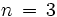 veces y calculemos la probabilidad del suceso "obtener 2 caras":
veces y calculemos la probabilidad del suceso "obtener 2 caras":
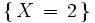 . ( Aqui el exito es que salga cara ). Existen tres posibilidades de que ocurra
. ( Aqui el exito es que salga cara ). Existen tres posibilidades de que ocurra
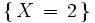 :
:
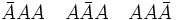
La diferencia entre estas tres posibilidades ( sucesos elementales ) es la prueba en que
ocurre el fracaso. En el primer caso, el fracaso ocurre en la primera prueba; en el
segundo caso ocurre en la segunda y en el tercer caso ocurre en la tercera.
Como estos sucesos son incompatibles, se tiene que:
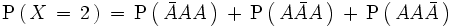
Por otra parte,
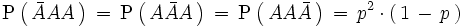 . Por ejemplo:
. Por ejemplo:
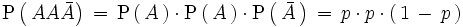
donde la primera igualdad es cierta porque los resultados de las tres pruebas son
independientes.
Así
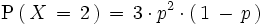
En general:
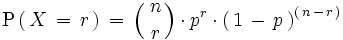
|
donde
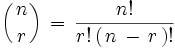
es el número de sucesos elementales que componen el suceso
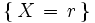 ( estos sucesos elementales tienen en común un mismo número de éxitos y de
fracasos y solo se diferencian en el orden en que ocurren los éxitos y los fracasos ).
( estos sucesos elementales tienen en común un mismo número de éxitos y de
fracasos y solo se diferencian en el orden en que ocurren los éxitos y los fracasos ).
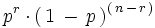 es la probabilidad de cada uno de estos sucesos elementales.
es la probabilidad de cada uno de estos sucesos elementales.
NOTA:
n!
es el factorial de
n
,
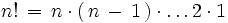
Ejemplo: Distribución binomial
¿Cual es la probabilidad de que en una familia con 5 hijos, 3 sean chicos y 2 chicas?
En este caso el experimento aleatorio consiste de
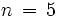 "pruebas". Cada una de estas pruebas es el nacimiento de un hijo. Supongamos que la probabilidad de que un hijo sea chico es
de
"pruebas". Cada una de estas pruebas es el nacimiento de un hijo. Supongamos que la probabilidad de que un hijo sea chico es
de
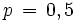 . Entonces, si
X
es el numero de hijos varones, se tiene que:
. Entonces, si
X
es el numero de hijos varones, se tiene que:
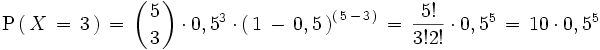
 , llamado fracaso.
, llamado fracaso.