Ejercicios: Números complejos (1ºBach)
De Wikipedia
Revisión de fecha 13:15 21 dic 2017; Ver revisión actual
← Revisión anterior | Revisión siguiente →
← Revisión anterior | Revisión siguiente →
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
|
Ejercicios de repaso |
Números complejos en forma binómica:
- Parte real y parte imaginaria de un número complejo.
- Complejos conjugados, iguales y opuestos.
- Ejercicio 1: Si el complejo a + 4i es conjugado con (2a - 1)+(3b + 2)i, calcula a2 + b2.
- Ejercicio 2: ¿Cuál es el valor de ab si (a - 3) - (b - 2)i es opuesto a 1 - (a - 1)i.
- Suma, resta, producto, cociente de números complejos.
- Ejercicio 3: Dados z1 = 2 - 3i y z2 = -1 - 2i, calcula z1 - z2.
- Ejercicio 4: Calcula (3 + 2i)·(5 + 3i).
- Ejercicio 5: Calcula (2 + 3i):(3 + i).
- Ejercicio 6: Calcula el valor de k para que el cociente (9 - ki):(3k - i) sea: a) real; b) Imaginario puro.
- Módulo de un número complejo.
- Ejercicio 7: Calcula
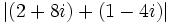 .
.
- Ejercicio 8: Calcula
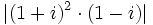 .
.
- Ejercicio 7: Calcula
- El plano complejo.
- Forma polar y forma trigonométrica de un número complejo. Conversión entre polar y binómica.
- Ejercicio 9: Convierte a forma polar: a)
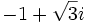 ; b)
; b) 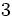 ; c)
; c) 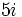
- Ejercicio 10: Convierte a forma binómica: a)
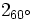 ; b)
; b) 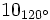 ; c)
; c) 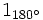 ; d)
; d) 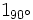 .
.
- Ejercicio 11: Calcula el opuesto y el conjugado de
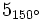 .
.
- Ejercicio 9: Convierte a forma polar: a)
- Producto, cociente, potencia y raíz en forma polar. Fórmula de Moivre.
- Ejercicio 12: Calcula
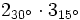 .
.
- Ejercicio 13: Calcula
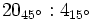 .
.
- Ejercicio 14: Calcula
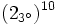 .
.
- Ejercicio 15: Expresa en forma binómica usando la fórmula de Moivre:
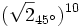 .
.
- Ejercicio 16: Resuelve en el conjunto de los números complejos:
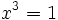 .
.
- Ejercicio 12: Calcula

