Plantilla:Raiz de primo es irracional
De Wikipedia
← Revisión anterior | Revisión siguiente →
Proposición
Si 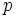 es un número primo, entonces el número
es un número primo, entonces el número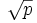 no es racional.
no es racional.
La demostración es análoga a la de que raíz de 2 es irracional.
Lo haremos, igualmente, "por reducción al absurdo". Supondremos que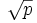 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que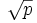 es racional, o sea, que existe una fracción que es igual a
es racional, o sea, que existe una fracción que es igual a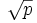 .
.
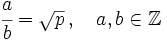
Elevamos al cuadrado los dos miembros de la igualdad:
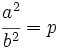
Multiplicamos por 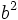 los dos miembros de la igualdad:
los dos miembros de la igualdad:
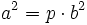 [1]
[1]Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces.
Como 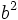 es un cuadrado perfecto, el factor
es un cuadrado perfecto, el factor 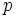 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor primo
o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor primo 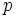 aparecería un número impar de veces en la descomposición del cuadrado perfecto
aparecería un número impar de veces en la descomposición del cuadrado perfecto 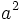 , lo cual no es posible.
, lo cual no es posible.
Ya hemos llegado al absurdo.
Videotutorial con otra demostración de la irracionalidad de la raíz de un número primo.

