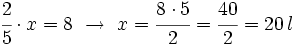El significado de las fracciones (1º ESO)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 122)
Introducción
| Los números enteros surgen porque no bastaba con los números naturales para cubrir ciertas necesidades. Sin embargo, tampoco los enteros son suficientes. Hay muchas situaciones en las que necesitamos representar unidades incompletas. Por ejemplo, cuando vas al supermercado y compras un cuarto de kilo de gambas, es porque tienes suficiente con solo una parte y no necesitas la totalidad del kilo; o cuando te dicen que el 99% de una medusa es agua, te queda muy claro que le falta muy poco para ser toda agua, pero que no lo es en su totalidad.
Para estos casos se inventaron las fracciones. Curiosamente, desde un punto de vista histórico, las necesidad de las fracciones fue cubierta antes que la necesidad de los números negativos. Probablemente sea más natural hablar de partes incompletas de algo (fracciones) que de partes que "no están" (negativos). Fueron los egipcios, hace más de 3500 años, los primeros en usar fracciones. No utilizaban la barra que usamos nosotros para separar numerador de denominador, sino un símbolo parecido a un ojo, y sólo usaban el 1 como numerador (fracciones unitarias), pero sentaron las bases de lo que hacemos nosotros hoy en día. |
Un toque divertido para empezar el tema:
Si no fuera por las fracciones ni Troncho ni Poncho ni nadie podría celebrar su cumpleaños.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Actividades en las que se resume lo que se va a ver en este tema.
Las fracciones
Cuando necesitamos expresar cantidades que representan unidades incompletas o partes de la unidad, además de los números decimales, disponemos de las fracciones.
- Una fracción es una expresión de la forma
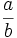 , o bien,
, o bien, 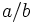 , donde
, donde  y
y  son números enteros, siendo
son números enteros, siendo 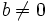 .
.
- Al número
 lo llamaremos numerador y al número
lo llamaremos numerador y al número  , denominador.
, denominador.
Una fracción se puede interpretar como una cantidad determinada de porciones que se toman de un todo dividido en partes iguales:
- El denominador sirve para representar las partes en que se divide la unidad.
- El numerador sirve para representar las porciones que tomamos.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según su valor, una fracción pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.
Esta definición nos da otra forma de interpretar a una fracción, ya que nos permite verla como una "división indicada" en las que el dividendo es el numerador y el cociente el denominador.
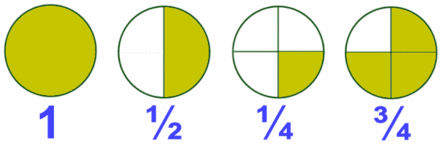
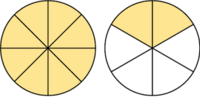
En la Fig. 2 tienes algunos ejemlos de fracciones representadas mendiante los llamados diagramas de tarta.
El valor de cada fracción se obtiene dividiendo el numerador entre el denominador:
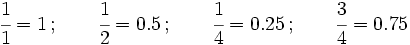
Fíjate que la unidad se puede representar mediante una fracción que tenga el mismo numerador que denominador.
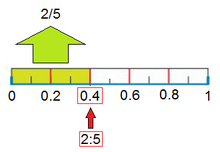
En la Fig. 3 está representada la fracción 2/5. Fíjate como al hacer la división 2:5=0.4, se obtienen 4 décimas, que ocupan la misma porción que la fracción 2/5. Es decir, una fracción equivale a una división indicada.
Concepto de fracción. Términos. ¿Cómo se leen?
Representación gráfica de fracciones y de su expresión decimal.
Concepto de fracción. Fracciones propias e impropias.
Concepto de fracción. Fracciones propias e impropias.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Fracciones unitarias (con numerador 1).
Importancia de dividir bien en partes iguales a la hora de representar fracciones gráficamente.
Tomando más de una parte del total.
Fracciones más grandes que la unidad.
Numerador y denominador de una fracción.
Fracciones en la recta numérica.
El plato de la cena de Vera está dividido en 3 secciones iguales. Si Vera puso brócoli en una sección del plato. ¿Qué fracci´´on del plato tiene brócoli?
Representa el punto 3/4 en la recta numérica.
Actividades sobre el significado de las fracciones.
Actividades sobre el significado de las fracciones.
- Actividad en la que se muestra y practica el concepto de fracción.
- Actividad en la que se explica y practica la representación gráfica de fracciones.
Actividades en las que se explica y practica cómo se lee una fracción.
Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica:
a) 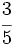 b)
b) 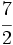 c)
c)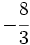 d)
d) 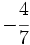 e)
e) 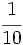 f)
f) 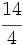
Compruéba las soluciones en la siguiente escena:
Corta figuras en partes iguales.
Reconoce fracciones.
Identifica numeradores y denominadores.
Las fracciones en la recta numérica
Fracciones unitarias en la recta numérica
Fracciones propias e impropias
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta.
Esto queda de manifiesto en la proposición y en los ejemplos que damos a continuación.
Proposición Toda fracción impropia, 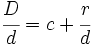
donde Demostración:
|
Ejemplo 1:
La fracción 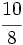 es impropia.
es impropia.
Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 4):
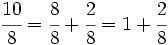
Ejemplo 2:
La frácción 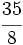 es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
Para ello, dividimos 35 entre 8:
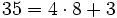
El dividendo 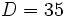 , el divisor
, el divisor 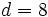 , el cociente
, el cociente 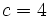 y el resto
y el resto 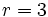 .
.
Aplicando la proposición anterior:
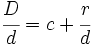
y sustituyendo cada letra por su valor:
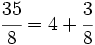
Actividades sobre el signo de las fracciones y sobre la descomposición de fracciones impropias como suma de un entero y una fracción propia.
Números mixtos
Una fracción mixta o número mixto es la representación de una fracción impropia como un número entero más una fracción propia, en la que se omite el signo de suma.
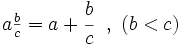
La fracción situada a la derecha del entero suele escribirse con una tipografía de menor tamaño para que no se confunda con una multiplicación de un número por una fracción.
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 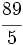
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 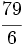
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 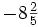
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
La fracción como operador
Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos.
Fracción de una cantidad
Para calcular una fracción a/b de una cantidad C se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por C).
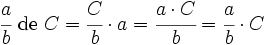
Ejemplo 1: Cálculo de la parte conocido el total
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada.
Ejemplo 2: Cálculo del total conocida la parte
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?
La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
Ejercicios y problemas
Problemas sencillos con fracciones resueltos.
Ejercicios de autoevaluación sobre fracciones.
Ejercicios y problemas de autoevaluación sobre fracciones.
|
Ejercicios propuestos: El significado de las fracciones |
|
Ejercicios propuestos: Problemas con fracciones |
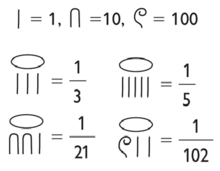
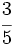 es una fracción propia porque 3 < 5.
es una fracción propia porque 3 < 5.
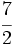 es una fracción impropia porque 7 > 2.
es una fracción impropia porque 7 > 2.
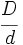 , se puede escribir como suma de un número entero y una fracción propia.
, se puede escribir como suma de un número entero y una fracción propia.
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
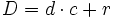
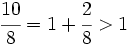
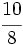 de la Fig. 4 hemos visto que se puede expresar mediante el número mixto
de la Fig. 4 hemos visto que se puede expresar mediante el número mixto 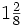 :
:
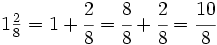
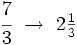 ; B)
; B) 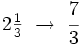
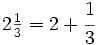
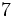

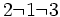 ; B)
; B) 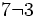
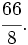
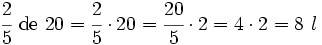
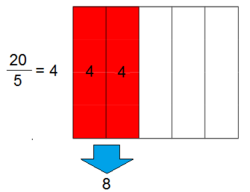
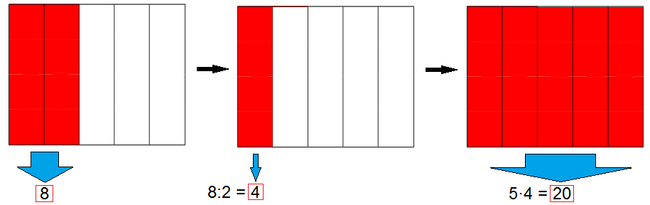
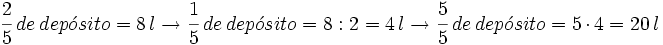
 = capacidad del depósito.
= capacidad del depósito.