Funciones de Proporcionalidad Inversa (4ºESO Académicas)
De Wikipedia
Revisión de fecha 17:28 15 ene 2019; Ver revisión actual
← Revisión anterior | Revisión siguiente →
← Revisión anterior | Revisión siguiente →
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
[editar]
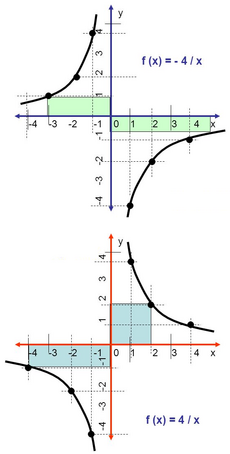
Funciones de proporcionalidad inversa
Sea 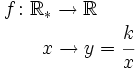 El numero Este tipo de funciones se llaman así porque si Propiedades de la función de proporcionalidad inversa Las funciones de proporcionalidad inversa
|
Representación de la familia de funciones de proporcionalidad inversa.
[editar]
Ejercicios propuestos
|
Ejercicios propuestos: Funciones de proporcionalidad inversa |
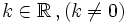 . Las función de proporcionalidad inversa se define como
. Las función de proporcionalidad inversa se define como
 recibe el nombre de constante de proporcionalidad inversa.
recibe el nombre de constante de proporcionalidad inversa.
 e
e  son cantidades correspondientes de dos magnitudes inversamente proporcionales, con constante de proporcionalidad
son cantidades correspondientes de dos magnitudes inversamente proporcionales, con constante de proporcionalidad 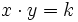 .
.
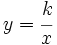 cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
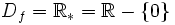 .
.
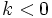 y decrecientes si
y decrecientes si 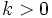 .
.