Funciones Exponenciales (4ºESO Académicas)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
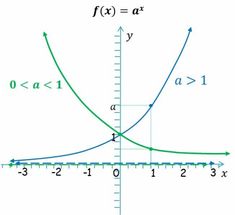
La función exponencial
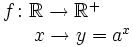
|
Propiedades de la función exponencial
Propiedades de la función exponencial Las funciones exponenciales de base
|
La función exponencial:
- Definición.
- Clasificación.
- Análisis y representación gráfica de la función exponencial de base 2.
La función exponencial:
- Definición.
- Clasificación.
- Análisis y representación gráfica de la función exponencial de base 1/2.
Valor inicial y razón común de una función exponencial.
Representa la función exponencial de base 3.
Representa la función exponencial de base 5.
Dadas tres gráficas de funciones exponenciales, elige la que se corresponde con una ecuación dada.
Problemas sobre modelos exponenciales vs. modelos lineales.
Representa gráficamente:
- a)
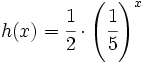
- b)
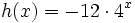
Escribe la expresión analítica de una función exponencial con valor inicial -2 y razón 1/7.
Escribe la expresión analítica de una función lineal y otra exponencial a partir de la tabla de valores dada en el video.
Escribe la expresión analítica de una función lineal y otra exponencial a partir de la gráfica dada en el video.
Escribe la expresión analítica de una función exponencial a partir de la tabla dada en el video.
Escribe la expresión analítica de una función exponencial a partir de la gráfica dada en el video.
Averigua para qué valor de  se cumple que
se cumple que 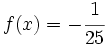 .
.
Una sustancia radioactiva se desintegra a una tasa del 3.5% por hora. ¿Qué porcentaje de sustancia queda después de 6 horas?
Averigua la expresión analítica de una función exponencial a partir de un enunciado y una tabla.
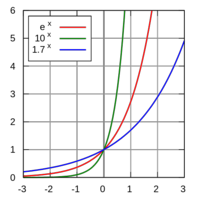
Representación de la familia de funciones exponenciales.
Modelos exponenciales vs. modelos lineales.
Crecimiento exponencial vs. crecimiento lineal en el tiempo.
Representación gráfica de funciones exponenciales.
Funciones exponenciales a partir de tablas y gráficas.
Utilidad de la función exponencial
Ejercicios propuestos
|
Ejercicios propuestos: Funciones exponenciales |
 . Se define la función exponencial de base
. Se define la función exponencial de base  como:
como:
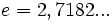 (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
(número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
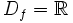 .
.
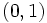 y
y 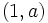 .
.
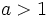 son crecientes
son crecientes
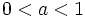 son decrecientes.
son decrecientes.