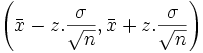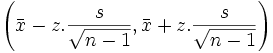Estimación por intervalos de confianza de medias y proporciones
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio Indice Estadistica | Inferencia | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Intervalo de confianza para la media
Ya vimos que la distribución muestral de las medias corresponde a:
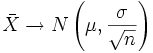
Queremos estimar la media poblacional μ a partir de la media muestral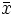 
, obteniendo para ello un intervalo de forma que tengamos una probabilidad alta (1-alfa)% de que la media poblacional esté en dicho intervalo.
Tipificando la expresión anterior:
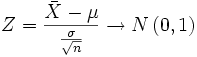
Si fijamos una probabilidad α, podemos obtener -z y z que limitan un área de valor 1 - α. Deshaciendo la tipificación obtenemos el intervalo de confianza para la media:
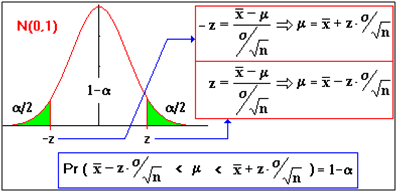
En Resumen:
Intervalo de confianza para la media poblacional μ con un nivel de confianza de 1 − α es:
a) Varianza poblacional conocida(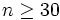
):
|
|
b) Varianza poblacional desconocida y muestras grandes (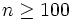
):
|
|
Donde z es el valor que en la distribución N(0,1) deja a su derecha un área de α / 2 (cuartil 1 − α / 2, s la desviación típica muestral y n el tamaño de la muestra.
