Contrastes de hipótesis sobre medias y proporciones
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio Indice Estadistica | Inferencia | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Empezaremos con un ejemplo del tipo de problema que queremos resolver:
Supongamos que se fabrican bombillas que tienen una duración normal X y una desviación tipica σ = 0.5. El fabricante afirma que la duración media de las bombillas es de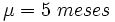 
.
Para contrastar esta afirmación se estudia una muestra de n = 25 bombillas y se halla la duración media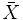 
de las 25 bombillas. Queremos ver si es cierto lo que afirma que lo llamaremos Hipótesis nula (H0).
El estadístico 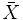se distribuye:
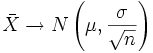
Luego si fijamos un nivel de confianza 1 − α = 0.95 el valor de 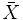estará en el intervalo
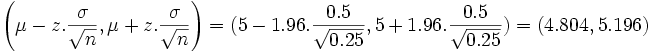con una probabilidad de 0.95.
