Fermat
De Wikipedia
| Revisión de 10:22 31 dic 2008 Coordinador (Discusión | contribuciones) (→Espiral de Fermat) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| + | [[Imagen:Fermat.jpg|thumb|Pierre de Fermat]] | ||
| '''Pierre de Fermat''' (1601 - 1665), jurista y matemático francés. | '''Pierre de Fermat''' (1601 - 1665), jurista y matemático francés. | ||
| Fue abogado en el Parlamento de Toulouse, en el sur de Francia, y matemático clave para el desarrollo del cálculo moderno. También hizo notables contribuciones a la geometría analítica. | Fue abogado en el Parlamento de Toulouse, en el sur de Francia, y matemático clave para el desarrollo del cálculo moderno. También hizo notables contribuciones a la geometría analítica. | ||
| Línea 5: | Línea 6: | ||
| ==Vida== | ==Vida== | ||
| + | [[Imagen:casaFermat.jpg|thumb|Casa de Beaumont-de-Lomagne donde nació Fermat; actual Museo Fermat]] | ||
| Fermat nació el 17 de agosto de 1601 en Beaumont-de-Lomagne, una ciudad situada a 58 kilómetros al noroeste de Toulouse, Francia. | Fermat nació el 17 de agosto de 1601 en Beaumont-de-Lomagne, una ciudad situada a 58 kilómetros al noroeste de Toulouse, Francia. | ||
| - | Poco se conoce de sus primeros años, excepto que estudió derecho, posiblemente en Toulouse y Burdeos. | + | El padre de Pierre Fermat era un rico comerciante de cuero y el segundo cónsul de Beaumont-de-Lomagne. Pierre tuvo un hermano y dos hermanas. Aunque hay poca evidencia respecto a su educación escolar debió de ser en monasterio franciscano local. |
| + | |||
| + | Asistió a la Universidad de Toulouse antes de mudarse a Burdeos, en la segunda mitad de los años 1620. En Burdeos comenzó sus primeras investigaciones serias en matemáticas. | ||
| + | |||
| + | Desde Burdeos Fermat fue a Orleáns donde estudió Derecho en la Universidad. Obtuvo una licenciatura en derecho civil, antes, en 1631, recibió el título de concejal en el Tribunal Superior de la Judicatura en Toulouse, que ocupó durante el resto de su vida. Debido al despacho que ahora ocupaba pasó a llamarse Pierre de Fermat en lugar de Pierre Fermat. Con dominio del latín, griego, italiano, y español, Fermat fue elogiado por su verso escrito en varios idiomas, y su consejo fue buscado con avidez en relación con la corrección de textos griegos. | ||
| + | |||
| + | Comunicó la mayor parte de su trabajo en las cartas a los amigos, a menudo con escasa o ninguna demostración de sus teoremas. Esto le permitió conservar su condición de "aficionado" al tiempo que obtubo el reconocimiento que él deseaba. Naturalmente, esto dio lugar a conflictos con colegas contemporáneos, como Descartes y Wallis. Desarrolló una estrecha relación con Pascal. | ||
| + | |||
| + | Anders Hald escribe que, "La base de las matemáticas de Fermat eran los tarados griegos clásicos combinados con los nuevos métodos algebraicos de [[Vieta]]." | ||
| Extremadamente prolífico, sus deberes profesionales y su particular forma de trabajar (sólo publicó una obra científica en vida) redujeron en gran medida el impacto de su obra. Fermat era un matemático que trabajaba la mayor parte del tiempo en soledad. Su único contacto con el resto de la comunidad matemática fue gracias a Marin Mersenne además de sus correspondencias con [[Pascal]]. Los resultados de Fermat fueron conocidos por otros pensadores europeos gracias a Mersenne, que los reenvió e hizo una amplia distribución. | Extremadamente prolífico, sus deberes profesionales y su particular forma de trabajar (sólo publicó una obra científica en vida) redujeron en gran medida el impacto de su obra. Fermat era un matemático que trabajaba la mayor parte del tiempo en soledad. Su único contacto con el resto de la comunidad matemática fue gracias a Marin Mersenne además de sus correspondencias con [[Pascal]]. Los resultados de Fermat fueron conocidos por otros pensadores europeos gracias a Mersenne, que los reenvió e hizo una amplia distribución. | ||
| Línea 18: | Línea 28: | ||
| *Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat. | *Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat. | ||
| *También se le ha dado su nombre a un cráter lunar de 39 km de diámetro. | *También se le ha dado su nombre a un cráter lunar de 39 km de diámetro. | ||
| - | *Películas: "La habitación de Fermat" | ||
| ==Obra== | ==Obra== | ||
| - | Interesado por las matemáticas, en 1629 abordó la tarea de reconstruir algunas de las demostraciones perdidas del matemático griego [[Apolonio]] relativas a los lugares geométricos; a tal efecto desarrollaría, contemporánea e independientemente de [[René Descartes]], un método algebraico para tratar cuestiones de geometría por medio de un sistema de coordenadas. | + | [[Imagen:manuscritoFermat.jpg|thumb|Manuscrito de Fermat del 4 de marzo de 1660 — Departamento de Archivos de Haute-Garonne, en Toulouse]] |
| + | Interesado por las matemáticas, en 1629 abordó la tarea de reconstruir algunas de las demostraciones perdidas del matemático griego [[Apolonio]] relativas a los lugares geométricos; a tal efecto desarrollaría, contemporánea e independientemente de [[Descartes]], un método algebraico para tratar cuestiones de geometría por medio de un sistema de coordenadas. | ||
| - | Diseñó un algoritmo de diferenciación mediante el cual pudo determinar los valores máximos y mínimos de una curva polinómica, amén de trazar las correspondientes tangentes, logros todos ellos que abrieron el camino al desarrollo ulterior del cálculo infinitesimal por [[Isaac Newton|Newton]] y [[Leibniz]]. | + | Diseñó un algoritmo de diferenciación mediante el cual pudo determinar los valores máximos y mínimos de una curva polinómica, amén de trazar las correspondientes tangentes, logros todos ellos que abrieron el camino al desarrollo ulterior del cálculo infinitesimal por [[Newton]] y [[Leibniz]]. |
| Tras asumir correctamente que cuando la luz se desplaza en un medio más denso su velocidad disminuye, demostró que el camino de un rayo luminoso entre dos puntos es siempre aquel que menos tiempo le cuesta recorrer; de dicho principio, que lleva su nombre, se deducen las leyes de la reflexión y la refracción. | Tras asumir correctamente que cuando la luz se desplaza en un medio más denso su velocidad disminuye, demostró que el camino de un rayo luminoso entre dos puntos es siempre aquel que menos tiempo le cuesta recorrer; de dicho principio, que lleva su nombre, se deducen las leyes de la reflexión y la refracción. | ||
| Línea 32: | Línea 42: | ||
| Fermat acostumbraba a escribir las soluciones a los problemas en el margen de los libros. Una vez escribió en su ejemplar del texto griego de ''La Aritmética'' de [[Diofanto]] (editada por Claude Gaspard Bachet de Méziriac en 1621) lo siguiente: | Fermat acostumbraba a escribir las soluciones a los problemas en el margen de los libros. Una vez escribió en su ejemplar del texto griego de ''La Aritmética'' de [[Diofanto]] (editada por Claude Gaspard Bachet de Méziriac en 1621) lo siguiente: | ||
| - | |||
| - | :"''Cubem autem in duos cubos, aut quadratoquadratorum in duos cuadratosquadratos, et generaliter nullam in infinitum ultra cuadratum potestandem in duos ejusdem nominis dividere: cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exigitas non caparet.''" | ||
| :"''Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El margen es demasiado pequeño para que la demostración quepa en él.''" | :"''Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El margen es demasiado pequeño para que la demostración quepa en él.''" | ||
| - | No se sabe si realmente halló la demostración ya que no dejó rastro de ella para que otros matemáticos pudiesen verificarla. Este problema mantuvo en vilo a los matemáticos durante más de tres siglos, hasta que en 1995 [[Wiles|Andrew Wiles]] encontró la demostración. Andrew utilizó para ello herramientas matemáticas que surgieron mucho después de la muerte de Fermat, luego éste debió haber encontrado la solución por otro camino, si es que lo hizo. En cualquier caso, Fermat tenía razón. | + | No se sabe si realmente halló la demostración ya que no dejó rastro de ella para que otros matemáticos pudiesen verificarla. Este problema, conocido como '''Último Teorema de Fermat''' mantuvo en vilo a los matemáticos durante más de tres siglos, hasta que en 1995 [[Wiles|Andrew Wiles]] encontró la demostración. Andrew utilizó para ello herramientas matemáticas que surgieron mucho después de la muerte de Fermat, luego éste debió haber encontrado la solución por otro camino, si es que lo hizo. En cualquier caso, Fermat tenía razón. |
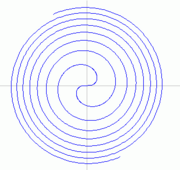
| === Espiral de Fermat === | === Espiral de Fermat === | ||
| + | [[Imagen:Fermat's spiral.png|thumb|right|Espiral de Fermat]] | ||
| La espiral de Fermat, denominada así en honor de Pierre de Fermat y también conocida como espiral parabólica, es una curva que responde a la siguiente ecuación: | La espiral de Fermat, denominada así en honor de Pierre de Fermat y también conocida como espiral parabólica, es una curva que responde a la siguiente ecuación: | ||
| Línea 56: | Línea 65: | ||
| Pierre de Fermat conjeturó que todos los números naturales de la forma | Pierre de Fermat conjeturó que todos los números naturales de la forma | ||
| <center><math> F_{n} = 2^{2^n} + 1 </math></center> | <center><math> F_{n} = 2^{2^n} + 1 </math></center> | ||
| - | con ''n'' natural eran números primos (después de todo, los cinco primeros términos, 3 (''n''=0), 5 (''n''=1), 17 (''n''=2), 257 (''n''=3) y 65537 (''n''=4) lo son), pero [[Euler]] probó que no era así en 1732. En efecto, al tomar ''n''=5 se obtiene un número compuesto: | + | con ''n'' natural eran números primos (después de todo, los cinco primeros términos, 3 (''n'' = 0), 5 (''n'' = 1), 17 (''n'' = 2), 257 (''n'' = 3) y 65537 (''n'' = 4) lo son), pero [[Euler]] probó que no era así en 1732. En efecto, al tomar ''n''=5 se obtiene un número compuesto: |
| <center><math> F_{5} = 2^{2^5} + 1 = 2^{32} + 1 = 4 294 967 297 = 641 \cdot 6 700 417 \; </math></center> | <center><math> F_{5} = 2^{2^5} + 1 = 2^{32} + 1 = 4 294 967 297 = 641 \cdot 6 700 417 \; </math></center> | ||
| 4294967297 es el número más pequeño que, siendo número de Fermat, no es primo. | 4294967297 es el número más pequeño que, siendo número de Fermat, no es primo. | ||
| - | Actualmente, sólo se conocen cinco números primos de Fermat, que son los que ya se conocían en tiempos del propio Fermat, y, a fecha de agosto de 2008 sólo se conoce la factorización completa de los doce primeros números de Fermat (desde ''n''=0 hasta ''n''=11). Estas son algunas de las conjeturas que existen hoy día sobre estos números: | + | Actualmente, sólo se conocen cinco números primos de Fermat, que son los que ya se conocían en tiempos del propio Fermat, y, a fecha de agosto de 2008 sólo se conoce la factorización completa de los doce primeros números de Fermat (desde ''n'' = 0 hasta ''n'' = 11). Estas son algunas de las conjeturas que existen hoy día sobre estos números: |
| *¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)? | *¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)? | ||
| *¿Existen infinitos primos de Fermat? | *¿Existen infinitos primos de Fermat? | ||
| === Pequeño teorema de Fermat === | === Pequeño teorema de Fermat === | ||
| - | [[Imagen:Pierre de Fermat.jpg|160px|thumb|right|[[Pierre de Fermat]].]] | + | El '''pequeño teorema de Fermat''' (1636) es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera: |
| - | El '''pequeño teorema de Fermat''' es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera: | + | |
| {{teorema | {{teorema | ||
| - | |1=Si ''p'' es un número primo, entonces, para cada número natural ''a'' , ''a''<sup>p</sup> ≡ ''a'' (mod ''p'') | + | |titulo=Pequeño Teorema de Fermat |
| - | |2=[[Pierre de Fermat]], 1636 | + | |enunciado=Si ''p'' es un número primo, entonces, para cada número natural ''a'' coprimo con ''p'' , ''a''<sup>p-1</sup> ≡ 1 (mod ''p''){{p}} |
| - | }} | + | O equivalentemente:{{p}} |
| + | ::Si ''p'' es un número primo, entonces, para cada número natural ''a'' , ''a''<sup>p</sup> ≡ ''a'' (mod ''p'') | ||
| + | |demo= | ||
| + | La prueba original, que se debe a [[Euler]] (y [[Leibniz]]), es sencilla, en términos de comprensión lógica, ya que sólo utiliza métodos elementales que una persona con nociones básicas de álgebra puede entender. Su demostración se basa en el principio de inducción, que consiste en demostar que si cierta propiedad ''P'' de los números naturales se cumple para ''n'' y también se cumple para ''n''+1, entonces se cumple para todo ''n''. | ||
| - | Aunque son equivalentes, el teorema suele ser presentado de esta otra forma: | + | Para la demostración también se utiliza la propiedad de que si ''p'' es un número primo, entonces el coeficiente binomial <math>\textstyle{p \choose n}</math> es divisible por ''p'', para todo ''n'', tal que 1≤ ''n''<''p''. |
| + | Esto es así puesto que el coeficiente binomial se define como: | ||
| - | {{teorema | + | <center><math>{p \choose n} = \frac{p!}{(p-n)!\cdot n!}</math></center> |
| - | |1=Si ''p'' es un número primo, entonces, para cada número natural ''a'' coprimo con ''p'' , ''a''<sup>p-1</sup> ≡ 1 (mod ''p'') | + | |
| - | |2=Pierre de Fermat, 1636 | + | Donde el signo ! corresponde al factorial de un número, que indica la multiplicación de todos los números naturales menores o iguales a dicho número, por ejemplo, ''p''! = ''p''·(''p''-1)·(''p''-2)·...·2·1. Puesto que en el |
| + | denominador, los factoriales de los números involucran números que son menores que el número primo ''p'', éstos no pueden contener ''p'' ni dividir al número primo ''p'' del numerador, así pues, el coeficiente es divisible por ''p''. | ||
| + | |||
| + | Dicho esto, la demostración consiste en los siguientes pasos: | ||
| + | |||
| + | * Supongamos que <math>\textstyle{p \mid n^p-n} \,\!</math> | ||
| + | |||
| + | * Utilizamos el binomio de Newton para expandir la potencia (''n'' + 1)<sup>p</sup>: | ||
| + | |||
| + | <center><math>(n+1)^p=\sum_{k=0}^{p}{p \choose k}n^{p-k}</math></center> | ||
| + | |||
| + | * Agrupando factores y reordenando la identidad: | ||
| + | |||
| + | <center><math>(n+1)^p-(n+1)=n^p-n+\sum_{k=1}^{p-1}{p \choose k}n^{p-k}</math></center> | ||
| + | |||
| + | * Por hipótesis, hemos supuesto que ''n''<sup>p</sup> - ''n'' es divisible por ''p'', y dado que todos los términos del sumatorio del miembro de la derecha son divisibles por ''p'', tenemos que ''p'' divide a (''n'' + 1)<sup>p</sup> - (''n'' + 1). | ||
| + | |||
| + | * Ahora bien, 1<sup>p</sup> - 1 es divisible por ''p'', por lo tanto 2<sup>p</sup> - 2 también es divisible por ''p'', y así sucesivamente. | ||
| + | |||
| + | Así queda demostrado. | ||
| }} | }} | ||
| Línea 89: | Línea 120: | ||
| --> | --> | ||
| Esto quiere decir que, si se eleva un número ''a'' a la ''p''-ésima potencia y al resultado se le resta ''a'', lo que queda es divisible por ''p'' (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía. | Esto quiere decir que, si se eleva un número ''a'' a la ''p''-ésima potencia y al resultado se le resta ''a'', lo que queda es divisible por ''p'' (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía. | ||
| + | |||
| + | Fermat estableció tal resultado en una carta a Frénicle de Bessy, pero como era habitual en él, omitió la prueba del mismo. | ||
| + | |||
| + | "Todo número primo ''mide'' una de las potencias menos uno de cualquier progresión en la que el exponente es un múltiplo del primo dado menos uno. (...) Y esta proposición es generalmente cierta para todas las progresiones y todos los números primos; le enviaría la prueba, si no temiese que es demasiado larga." | ||
| + | |||
| + | La primera demostración publicada se debe a [[Euler]] en 1736 en un artículo titulado ''Theorematum Quorundam ad Números Primos Spectantium Demonstratio''. Daría otras dos demostraciones más a lo largo de su vida, aunque era la primera de todas ellas la misma que había en un manuscrito personal de [[Leibniz]], escrito sobre 1683 y que nunca llegó a publicar. [[Gauss]] publicaría otra prueba más en su libro ''Disquisitiones arithmeticae'' en 1801. | ||
| + | |||
| + | Aunque actualmente lo conozcamos como ''pequeño teorema de Fermat'', lo cierto es que hasta el siglo XX fue conocido como ''teorema de Fermat'', como recoge por ejemplo [[Gauss]] en su libro ''Disquisitiones arithmeticae''. El término ''pequeño teorema de Fermat'', tal como lo conocemos actualmente, fue usado por primera vez por el matemático alemán Kurt Hensel en 1913 en su libro ''Zahlentheorie''. | ||
| === Principio de Fermat === | === Principio de Fermat === | ||
| - | {{AP|Principio de Fermat}} | + | El Principio de Fermat en óptica establece: |
| + | |||
| + | ''El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es un mínimo'' | ||
| + | |||
| + | El principio fue enunciado de esta forma por Fermat. Pero este enunciado no es completo y no cubre todos los casos, por lo que existe una forma moderna del principio de Fermat. Esta dice que | ||
| + | |||
| + | ''El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es estacionario respecto a posibles variaciones de la trayectoria'' | ||
| + | |||
| + | Esto quiere decir que, si se expresa el tiempo t en función de un parámetro s (el espacio recorrido), el trayecto recorrido por la luz será aquel en que ''dt/ds''= 0, es decir, ''t'' será un mínimo, un máximo o un punto de inflexión de la curva que representa ''t'' en función de ''s''. La carácterística importante, como dice el enunciado, es que los trayectos próximos al ''verdadero'' requieren tiempos aproximadamente iguales (esto es forzosamente cierto si t(s) es una función continua y ''dt/ds''= 0). | ||
| === Último teorema de Fermat === | === Último teorema de Fermat === | ||
| + | {{teorema | ||
| + | |titulo=Último Teorema de Fermat | ||
| + | |enunciado=Si <math>n</math> es un número entero mayor que 2 (o sea, <math>n</math> > 2), entonces no existen números enteros <math>a</math>, <math>b</math> y <math>c</math> (excepto las soluciones triviales, <math>a=0</math> ó <math>b=0</math> ó <math>c=0</math>) tales que cumplan la igualdad: | ||
| + | |||
| + | <center><math> c^n = a^n + b^n \,</math></center> | ||
| + | }} | ||
| + | |||
| + | Fermat escribió en el margen de su copia del libro ''Arithmetica'' de [[Diofanto]], traducido por Claude Gaspar Bachet, en el problema que trata sobre la división de un cuadrado como suma de dos cuadrados (<math>c^2 = a^2 + b^2</math>) | ||
| + | |||
| + | <blockquote style="font-style:italic;">Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos,<br />et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem <br />nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. <br />Hanc marginis exigitas non caperet.</blockquote> | ||
| + | |||
| + | que traducido dice: | ||
| + | |||
| + | <blockquote style="font-style:italic;">Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados,<br />o en general, cualquier potencia superior a dos en dos potencias del mismo grado;<br /> he descubierto una demostración maravillosa de esta afirmación.<br />Pero este margen es demasiado angosto para contenerla.</blockquote> | ||
| + | |||
| + | El primer matemático que consiguió avanzar sobre este teorema fue [[Euler|Leonhard Euler]] que demostró el caso <math>n = 3</math>. | ||
| + | |||
| + | En el año 1995 el matemático [[Wiles|Andrew Wiles]], en un artículo de 98 páginas publicado en ''Annals of mathematics'' (1995), demostró el Teorema de Taniyama-Shimura, anteriormente una conjetura, que engarza las ecuaciones modulares y las elípticas. De este trabajo, se desprende la demostración del Último Teorema de Fermat. (Wiles, Andrew. ''Modular elliptic curves and Fermat's last theorem''. Ann. of Math. (2) 141 (1995), no. 3, 443--551). Aunque el artículo original de Wiles contenía un error, pudo ser corregido en colaboración con el matemático Richard Taylor y la demostración fue posteriormente aceptada. | ||
| - | <!--Si n es un número natural mayor que dos, no existe ningún trío de números naturales ''x, y,z'', tales que <math>x^''n''+y^''n''=z^''n''</math> | ||
| - | Es decir, por ejemplo, loa suma de dos cubos nunca es un cubo, y en general, la suma de dos potencias iguales mayores de dos, nunca será igual a otra potencia igual. | ||
| - | --> | ||
| === Libros === | === Libros === | ||
| - | *''El enigma de Fermat''. [[Simon Singh]]. ISBN 84-08-02375-6. | + | *''El enigma de Fermat''. Simon Singh. ISBN 84-08-02375-6. |
| - | *''El último teorema de Fermat''.[[Simon Singh]]. ISBN 958-04-4865-5 | + | *''El último teorema de Fermat''.Simon Singh. ISBN 958-04-4865-5 |
| - | *''Fermat: el mago de los números''. [[Blas Torrecillas Jover]]. ISBN 84-930719-2-7. | + | *''Fermat: el mago de los números''. Blas Torrecillas Jover. ISBN 84-930719-2-7. |
| ==Video== | ==Video== | ||
Revisión actual
Pierre de Fermat (1601 - 1665), jurista y matemático francés. Fue abogado en el Parlamento de Toulouse, en el sur de Francia, y matemático clave para el desarrollo del cálculo moderno. También hizo notables contribuciones a la geometría analítica.
Fermat es mejor conocido por su Enigma, una abstracción del Teorema de Pitágoras, también conocido como Último Teorema de Fermat, que torturó a los matemáticos durante aproximadamente 350 años, hasta que fue resuelto en 1995. Junto con René Descartes, Fermat fue uno de los líderes matemáticos de la primera mitad del siglo XVII. Independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. A través de su correspondencia con Blaise Pascal, fue co-fundador de la teoría de probabilidades.
Tabla de contenidos |
Vida
Fermat nació el 17 de agosto de 1601 en Beaumont-de-Lomagne, una ciudad situada a 58 kilómetros al noroeste de Toulouse, Francia.
El padre de Pierre Fermat era un rico comerciante de cuero y el segundo cónsul de Beaumont-de-Lomagne. Pierre tuvo un hermano y dos hermanas. Aunque hay poca evidencia respecto a su educación escolar debió de ser en monasterio franciscano local.
Asistió a la Universidad de Toulouse antes de mudarse a Burdeos, en la segunda mitad de los años 1620. En Burdeos comenzó sus primeras investigaciones serias en matemáticas.
Desde Burdeos Fermat fue a Orleáns donde estudió Derecho en la Universidad. Obtuvo una licenciatura en derecho civil, antes, en 1631, recibió el título de concejal en el Tribunal Superior de la Judicatura en Toulouse, que ocupó durante el resto de su vida. Debido al despacho que ahora ocupaba pasó a llamarse Pierre de Fermat en lugar de Pierre Fermat. Con dominio del latín, griego, italiano, y español, Fermat fue elogiado por su verso escrito en varios idiomas, y su consejo fue buscado con avidez en relación con la corrección de textos griegos.
Comunicó la mayor parte de su trabajo en las cartas a los amigos, a menudo con escasa o ninguna demostración de sus teoremas. Esto le permitió conservar su condición de "aficionado" al tiempo que obtubo el reconocimiento que él deseaba. Naturalmente, esto dio lugar a conflictos con colegas contemporáneos, como Descartes y Wallis. Desarrolló una estrecha relación con Pascal.
Anders Hald escribe que, "La base de las matemáticas de Fermat eran los tarados griegos clásicos combinados con los nuevos métodos algebraicos de Vieta."
Extremadamente prolífico, sus deberes profesionales y su particular forma de trabajar (sólo publicó una obra científica en vida) redujeron en gran medida el impacto de su obra. Fermat era un matemático que trabajaba la mayor parte del tiempo en soledad. Su único contacto con el resto de la comunidad matemática fue gracias a Marin Mersenne además de sus correspondencias con Pascal. Los resultados de Fermat fueron conocidos por otros pensadores europeos gracias a Mersenne, que los reenvió e hizo una amplia distribución.
Murió en Castres, Francia, el 12 de enero de 1665.
Curiosidades
- La mansión del siglo XV donde nació es en la actualidad un museo.
- La escuela más antigua y prestigiosa de Toulouse se llama Pierre de Fermat y en ella se imparten clases de ingeniería y comercio. Está situada entre las diez mejores de Francia para clases preparatorias.
- Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat.
- También se le ha dado su nombre a un cráter lunar de 39 km de diámetro.
Obra
Interesado por las matemáticas, en 1629 abordó la tarea de reconstruir algunas de las demostraciones perdidas del matemático griego Apolonio relativas a los lugares geométricos; a tal efecto desarrollaría, contemporánea e independientemente de Descartes, un método algebraico para tratar cuestiones de geometría por medio de un sistema de coordenadas.
Diseñó un algoritmo de diferenciación mediante el cual pudo determinar los valores máximos y mínimos de una curva polinómica, amén de trazar las correspondientes tangentes, logros todos ellos que abrieron el camino al desarrollo ulterior del cálculo infinitesimal por Newton y Leibniz.
Tras asumir correctamente que cuando la luz se desplaza en un medio más denso su velocidad disminuye, demostró que el camino de un rayo luminoso entre dos puntos es siempre aquel que menos tiempo le cuesta recorrer; de dicho principio, que lleva su nombre, se deducen las leyes de la reflexión y la refracción.
En 1654, y como resultado de una larga correspondencia, desarrolló con su colega Blaise Pascal los principios de la teoría de probabilidad.
Otro campo en el que realizó destacadas aportaciones fue el de la teoría de números, en la que empezó a interesarse tras consultar una edición de la Aritmética de Diofanto. De su trabajo en dicho campo se derivaron importantes resultados relacionados con las propiedades de los números primos, muchas de las cuales quedaron expresadas en forma de simples proposiciones y teoremas. Desarrolló también un ingenioso método de demostración que denominó «del descenso infinito».
Fermat acostumbraba a escribir las soluciones a los problemas en el margen de los libros. Una vez escribió en su ejemplar del texto griego de La Aritmética de Diofanto (editada por Claude Gaspard Bachet de Méziriac en 1621) lo siguiente:
- "Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El margen es demasiado pequeño para que la demostración quepa en él."
No se sabe si realmente halló la demostración ya que no dejó rastro de ella para que otros matemáticos pudiesen verificarla. Este problema, conocido como Último Teorema de Fermat mantuvo en vilo a los matemáticos durante más de tres siglos, hasta que en 1995 Andrew Wiles encontró la demostración. Andrew utilizó para ello herramientas matemáticas que surgieron mucho después de la muerte de Fermat, luego éste debió haber encontrado la solución por otro camino, si es que lo hizo. En cualquier caso, Fermat tenía razón.
Espiral de Fermat
La espiral de Fermat, denominada así en honor de Pierre de Fermat y también conocida como espiral parabólica, es una curva que responde a la siguiente ecuación:
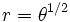
Es un caso particular de la espiral de Arquímedes.
Números amigos
Los pitagóricos observaron una rara relación entre los números 220 y 284: la suma de los divisores de cada uno de ellos, salvo el propio número, es el otro. Los denominaron números amigos. Durante muchos siglos, la pareja 220 y 284 fueron los únicos amigos conocidos, hasta que en 1636 Fermat descubrió que 17.296 y 18.416 también lo son. En 1638 Descartes, colega y competidor de Fermat, encontró la tercera pareja: 9.363.584 y 9.437.056
Números primos
Un número de Fermat, nombrado en honor a Pierre de Fermat, quien fue el primero que estudió estos números, es un número natural de la forma:
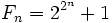
donde n es natural. De particular interés son los números primos de Fermat.
Pierre de Fermat conjeturó que todos los números naturales de la forma
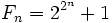
con n natural eran números primos (después de todo, los cinco primeros términos, 3 (n = 0), 5 (n = 1), 17 (n = 2), 257 (n = 3) y 65537 (n = 4) lo son), pero Euler probó que no era así en 1732. En efecto, al tomar n=5 se obtiene un número compuesto:
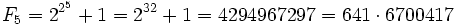
4294967297 es el número más pequeño que, siendo número de Fermat, no es primo.
Actualmente, sólo se conocen cinco números primos de Fermat, que son los que ya se conocían en tiempos del propio Fermat, y, a fecha de agosto de 2008 sólo se conoce la factorización completa de los doce primeros números de Fermat (desde n = 0 hasta n = 11). Estas son algunas de las conjeturas que existen hoy día sobre estos números:
- ¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)?
- ¿Existen infinitos primos de Fermat?
Pequeño teorema de Fermat
El pequeño teorema de Fermat (1636) es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera:
Pequeño Teorema de Fermat
Si p es un número primo, entonces, para cada número natural a coprimo con p , ap-1 ≡ 1 (mod p) O equivalentemente:
- Si p es un número primo, entonces, para cada número natural a , ap ≡ a (mod p)
La prueba original, que se debe a Euler (y Leibniz), es sencilla, en términos de comprensión lógica, ya que sólo utiliza métodos elementales que una persona con nociones básicas de álgebra puede entender. Su demostración se basa en el principio de inducción, que consiste en demostar que si cierta propiedad P de los números naturales se cumple para n y también se cumple para n+1, entonces se cumple para todo n.
Para la demostración también se utiliza la propiedad de que si p es un número primo, entonces el coeficiente binomial 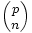 es divisible por p, para todo n, tal que 1≤ n<p.
Esto es así puesto que el coeficiente binomial se define como:
es divisible por p, para todo n, tal que 1≤ n<p.
Esto es así puesto que el coeficiente binomial se define como:
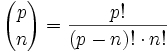
Donde el signo ! corresponde al factorial de un número, que indica la multiplicación de todos los números naturales menores o iguales a dicho número, por ejemplo, p! = p·(p-1)·(p-2)·...·2·1. Puesto que en el denominador, los factoriales de los números involucran números que son menores que el número primo p, éstos no pueden contener p ni dividir al número primo p del numerador, así pues, el coeficiente es divisible por p.
Dicho esto, la demostración consiste en los siguientes pasos:
- Supongamos que
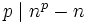
- Utilizamos el binomio de Newton para expandir la potencia (n + 1)p:
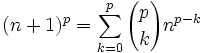
- Agrupando factores y reordenando la identidad:
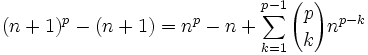
- Por hipótesis, hemos supuesto que np - n es divisible por p, y dado que todos los términos del sumatorio del miembro de la derecha son divisibles por p, tenemos que p divide a (n + 1)p - (n + 1).
- Ahora bien, 1p - 1 es divisible por p, por lo tanto 2p - 2 también es divisible por p, y así sucesivamente.
Esto quiere decir que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía.
Fermat estableció tal resultado en una carta a Frénicle de Bessy, pero como era habitual en él, omitió la prueba del mismo.
"Todo número primo mide una de las potencias menos uno de cualquier progresión en la que el exponente es un múltiplo del primo dado menos uno. (...) Y esta proposición es generalmente cierta para todas las progresiones y todos los números primos; le enviaría la prueba, si no temiese que es demasiado larga."
La primera demostración publicada se debe a Euler en 1736 en un artículo titulado Theorematum Quorundam ad Números Primos Spectantium Demonstratio. Daría otras dos demostraciones más a lo largo de su vida, aunque era la primera de todas ellas la misma que había en un manuscrito personal de Leibniz, escrito sobre 1683 y que nunca llegó a publicar. Gauss publicaría otra prueba más en su libro Disquisitiones arithmeticae en 1801.
Aunque actualmente lo conozcamos como pequeño teorema de Fermat, lo cierto es que hasta el siglo XX fue conocido como teorema de Fermat, como recoge por ejemplo Gauss en su libro Disquisitiones arithmeticae. El término pequeño teorema de Fermat, tal como lo conocemos actualmente, fue usado por primera vez por el matemático alemán Kurt Hensel en 1913 en su libro Zahlentheorie.
Principio de Fermat
El Principio de Fermat en óptica establece:
El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es un mínimo
El principio fue enunciado de esta forma por Fermat. Pero este enunciado no es completo y no cubre todos los casos, por lo que existe una forma moderna del principio de Fermat. Esta dice que
El trayecto seguido por la luz al propagarse de un punto a otro es tal que el tiempo empleado en recorrerlo es estacionario respecto a posibles variaciones de la trayectoria
Esto quiere decir que, si se expresa el tiempo t en función de un parámetro s (el espacio recorrido), el trayecto recorrido por la luz será aquel en que dt/ds= 0, es decir, t será un mínimo, un máximo o un punto de inflexión de la curva que representa t en función de s. La carácterística importante, como dice el enunciado, es que los trayectos próximos al verdadero requieren tiempos aproximadamente iguales (esto es forzosamente cierto si t(s) es una función continua y dt/ds= 0).
Último teorema de Fermat
Último Teorema de Fermat
Si n es un número entero mayor que 2 (o sea, n > 2), entonces no existen números enteros a, b y c (excepto las soluciones triviales, a = 0 ó b = 0 ó c = 0) tales que cumplan la igualdad:
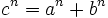
{{{demo}}}
Fermat escribió en el margen de su copia del libro Arithmetica de Diofanto, traducido por Claude Gaspar Bachet, en el problema que trata sobre la división de un cuadrado como suma de dos cuadrados (c2 = a2 + b2)
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos,
et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem
nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi.
Hanc marginis exigitas non caperet.
que traducido dice:
Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados,
o en general, cualquier potencia superior a dos en dos potencias del mismo grado;
he descubierto una demostración maravillosa de esta afirmación.
Pero este margen es demasiado angosto para contenerla.
El primer matemático que consiguió avanzar sobre este teorema fue Leonhard Euler que demostró el caso n = 3.
En el año 1995 el matemático Andrew Wiles, en un artículo de 98 páginas publicado en Annals of mathematics (1995), demostró el Teorema de Taniyama-Shimura, anteriormente una conjetura, que engarza las ecuaciones modulares y las elípticas. De este trabajo, se desprende la demostración del Último Teorema de Fermat. (Wiles, Andrew. Modular elliptic curves and Fermat's last theorem. Ann. of Math. (2) 141 (1995), no. 3, 443--551). Aunque el artículo original de Wiles contenía un error, pudo ser corregido en colaboración con el matemático Richard Taylor y la demostración fue posteriormente aceptada.
Libros
- El enigma de Fermat. Simon Singh. ISBN 84-08-02375-6.
- El último teorema de Fermat.Simon Singh. ISBN 958-04-4865-5
- Fermat: el mago de los números. Blas Torrecillas Jover. ISBN 84-930719-2-7.
Video
Video: Fermat, el margen más famoso de la historia (22´)
A principios de siglo XVII un abogado, aficionado a las matemáticas va a lanzar una serie de retos, basados en los números más simples, los enteros, a toda la comunidad matemática. Es Pierre de Fermat. La inspiración para estos retos la encontró en un antiguo libro de matemáticas escrito allá por el siglo III, la Aritmética de Diofanto. En uno de sus márgenes Fermat va a escribir una frase que se convertirá en una de las más atractivas de la historia de las matemáticas. Su famoso último teorema:
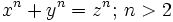 ”
”