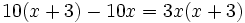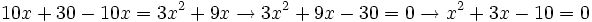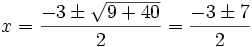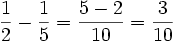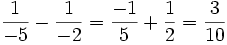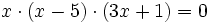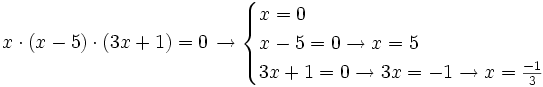Otros tipos de ecuaciones (4ºESO Académicas)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 21:49 1 ene 2009

Menú:

Enlaces internos	Para repasar	Enlaces externos
Indice Descartes Manual Casio	Test de Álgebra	WIRIS Calculadora

Tabla de contenidos

1 Ecuaciones bicuadradas
2 Ecuaciones con la x en el denominador
3 Ecuaciones con radicales
4 Ecuaciones factorizadas:

Ecuaciones bicuadradas

Las ecuaciones bicuadradas Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma

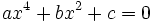
$ax^4 + bx^2 +c = 0\,\!$

El truco para resolverlas es hacer el cambio de variable 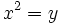$x^2=y\,\!$ entonces la ecuación quedará como una de segundo grado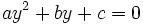 $ay^2 + by + c = 0 \,\!$

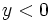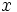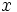
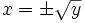
La resolvemos, y desechamos los valores de $y<0\,\!$ que no dan solución en las $x\,\!$ y nos queamos con las soluciones positivas que nos daran dos valores de $x\,\!$ $x=\pm \sqrt{y}$

Ejemplo: Ecuaciones bicuadradas

Resuelve las ecuaciones:

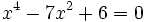
a) $x^4 - 7x^2 + 6 = 0\;\!$

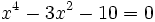
b) $x^4 - 3x^2 - 10 = 0\;\!$

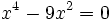
c) $x^4 - 9x^2 = 0 \;\!$

Solución:

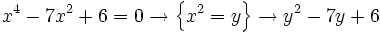
a) $x^4 - 7x^2 + 6 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-7y+6$

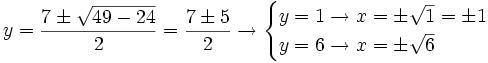
$y = \frac{7 \pm \sqrt{49-24}}{2}=\frac{7 \pm 5}{2} \rightarrow \begin{cases} y=1 \rightarrow x= \pm \sqrt 1 = \pm 1 \\ y=6 \rightarrow x= \pm \sqrt 6 \end{cases}$

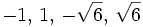
Soluciones: $-1,\, 1,\, -\sqrt 6,\, \sqrt 6\,\!$

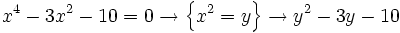
b) $x^4 - 3x^2 - 10 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-3y-10$

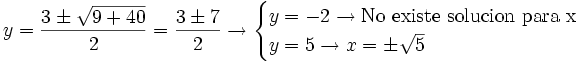
$y = \frac{3 \pm \sqrt{9+40}}{2}=\frac{3 \pm 7}{2} \rightarrow \begin{cases} y=-2 \rightarrow \mbox {No existe solucion para x} \\ y=5 \rightarrow x= \pm \sqrt 5 \end{cases}$

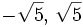
Soluciones: $-\sqrt 5,\, \sqrt 5\,\!$

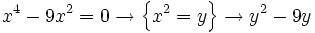
c) $x^4 - 9x^2 = 0 \rightarrow \left \{ x^2=y \right \}\rightarrow y^2-9y$

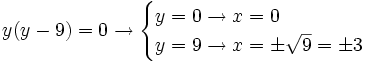
$y(y-9)=0 \rightarrow \begin{cases} y=0 \rightarrow x= 0 \\ y=9 \rightarrow x= \pm \sqrt 9 = \pm 3 \end{cases}$

Soluciones: $0,\, -3,\, 3\,\!$

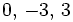
Ecuaciones con la x en el denominador

Las ecuaciones que tienen la incógnita en el denominador, laspuedes resolver de forma análoga a las que tienen números en el denominador, es decir, haciendo el mínimo común múltiplo de los denominadores. A continuación se divide el m.c.m. entre cada denominador y se multiplica el resultado por su respectivo numerador, Esto se hace con los dos miembros de la ecuación.De esta forma desaparecen los denominadores y la ecuación resultante ya es más sencilla de resolver.

En estos procesos de multiplicar los miembros de la ecuación por polinomios, pueden aparecer soluciones falsas. Por tanto, al terminar, siempre debemos comprobar todas las posibles soluciones obtenidas.

Ejemplo: Ecuaciones con x en el denominador

Resuelve las ecuación: 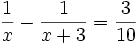$\frac{1} {x}- \frac{1} {x+3} = \frac{3} {10}$

Solución:

El m.c.m. de los denominadores es 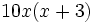$10x(x+3)\,\!$ . Lo dividimos por cada denominador y multiplicamos el resultado por el numerador, de manera que los denominadores desaparecen:

$10(x+3)-10x = 3x(x+3)\;$

Simplificamos la ecuación resultante:

$10x+30-10x = 3x^2+9x \rightarrow 3x^2+9x-30 = 0 \rightarrow x^2+3x-10 = 0$

Y la resolvemos:

$x = \frac{-3 \pm \sqrt{9+40}} {2} = \frac{-3 \pm 7} {2}$

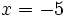Hay dos soluciones: $x=2\;$ y $x=-5\;$ . Ambas se deben comprobar en la ecuación inicial y resultan ser válidas:

$\frac{1} {2}- \frac{1} {5}= \frac{5-2} {10} = \frac{3} {10}$

$\frac{1} {-5}- \frac{1} {-2}= \frac{-1} {5}+ \frac{1} {2} = \frac{3} {10}$

Ecuaciones con radicales

Hay veces que nos encontraremos con ecuaciónes que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.

Al elevar al cuadrado para buscar la solución, aparecen soluciones erroneas y hay que rechazarlas. Para ello, hay que hacer la comprobación en la ecuación inicial para detectarlas.

Ejemplo: Ecuaciones con radicales

Resuelve las ecuaciones:

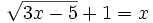
a) $\sqrt{3x-5} +1=x\;\!$

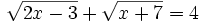
b) $\sqrt{2x-3} + \sqrt{x+7} = 4 \;\!$

Solución:

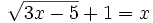
a) $\sqrt{3x-5} +1=x$

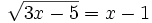$\sqrt{3x-5}=x-1$ Se elevan al cuadrado los dos lados de la ecuación:

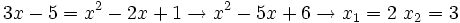
$3x-5=x^2-2x+1 \rightarrow x^2 -5x + 6 \rightarrow x_1=2 \ x_2=3 \,\!$

Comprobación: 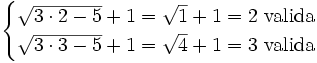$\b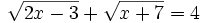egin{cases} \sqrt{3 \cdot 2 - 5} + 1 = \sqrt{1} + 1 = 2 \ \mbox{valida} \\ \sqrt{3 \cdot 3 - 5} + 1 = \sqrt{4} + 1 = 3 \ \mbox{valida} \end{cases}$

b) $\sqrt{2x-3} + \sqrt{x+7} = 4$ Despejamos la primera raíz (Podíamos haber empezado por la segunda)

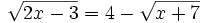$\sqrt{2x-3} = 4 - \sqrt{x+7}$ Se elevan al cuadrado los dos lados del igual

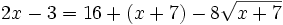$2x-3 = 16 + (x+7) -8\sqrt{x+7}$ Aislamos la raíz

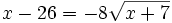$x -26 = -8\sqrt{x+7}$ Se elevan al cuadrado los dos lados del igual

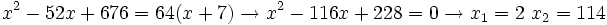
$x^2-52x+676=64(x+7) \rightarrow x^2-116x+228=0 \rightarrow x_1=2 \ x_2=114$

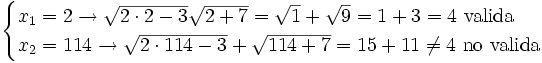
Comprobación $\begin{cases} x_1=2 \rightarrow \sqrt{2 \cdot 2 -3} \sqrt{2+7}=\sqrt{1}+\sqrt{9} = 1+3=4 \ \mbox{valida} \\ x_2=114 \rightarrow \sqrt{2 \cdot 114 - 3} + \sqrt{114+7}=15+11 \ne 4 \ \mbox{no valida} \end{cases}$

Ecuaciones factorizadas: 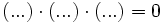$(...) \cdot (...) \cdot (...) = 0$

Para que un producto sea cero basta con que uno de los factores sea cero. Entonces para resolver una ecuación de este tipo, cada paréntesis se iguala a cero y se resuelve dicha ecuación.

Ejemplo: Ecuación factorizada

Resuelve la ecuación:

$x \cdot (x-5)\cdot (3x+1)=0\;\!$

Solución:

$x \cdot (x-5)\cdot (3x+1)=0\;\! \rightarrow \begin{cases} x = 0 \\ x-5=0 \rightarrow x=5 \\ 3x+1=0 \rightarrow 3x=-1 \rightarrow x= \frac{-1} {3} \end{cases}$

Obtenido de "http://maralboran.org/wikipedia/index.php/Otros_tipos_de_ecuaciones_%284%C2%BAESO_Acad%C3%A9micas%29"

Categorías: Matemáticas | Álgebra

 ==Ecuaciones con radicales==
-{{Caja_Amarilla|texto=Hay veces que nos encontraremos con ecuaciónes que tienen la x dentro de raices cuadradas para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.
+{{Caja_Amarilla|texto=Hay veces que nos encontraremos con ecuaciónes que tienen la x dentro de raices cuadradas. Para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.
-Al elevar al cuadrado y buscar la solución aparecen soluciones debidas al proceso (de elevar al cuadrado para eliminar las raíces) estas soluciones son erroneas y hay que rechazarlas. Hay que hacer la comprobación en la ecuación inicial '''siempre''' para detectar las soluciones erroneas.
+Al elevar al cuadrado para buscar la solución, aparecen soluciones erroneas y hay que rechazarlas. Para ello, hay que '''hacer la comprobación''' en la ecuación inicial para detectarlas.
 }}
 {{p}}
 {{Ejemplo|titulo=Ejemplo: ''Ecuaciones con radicales
 |enunciado=Resuelve las ecuaciones:
-<center><math>\sqrt{3x-5} +1=x
+::a) <math>\sqrt{3x-5} +1=x\;\! </math>
-\;\! </math></center>
-<center><math>\sqrt{2x-3} + \sqrt{x+7} = 4 \;\! </math></center>
+::b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4 \;\! </math>
 |sol=
-<math>\sqrt{3x-5} +1=x</math>
-<math>\sqrt{3x-5}=x-1</math> Se elevan al cuadrado los dos lados del igual
+a) <math>\sqrt{3x-5} +1=x</math>
+<math>\sqrt{3x-5}=x-1</math> Se elevan al cuadrado los dos lados de la ecuación:
 <math>3x-5=x^2-2x+1 \rightarrow x^2 -5x + 6 \rightarrow x_1=2 \ x_2=3 \,\!</math>
 Comprobación: <math>\begin{cases} \sqrt{3 \cdot 2 - 5} + 1 = \sqrt{1} + 1 = 2 \ \mbox{valida} \\ \sqrt{3 \cdot 3 - 5} + 1 = \sqrt{4} + 1 = 3 \ \mbox{valida} \end{cases}</math>
+----
+b) <math>\sqrt{2x-3} + \sqrt{x+7} = 4</math> Despejamos la primera raíz (Podíamos haber empezado por la segunda)
-<math>\sqrt{2x-3} + \sqrt{x+7} = 4</math> Despejamos la primera raíz (Podíamos haber empezado por la segunda)
 <math>\sqrt{2x-3} = 4 - \sqrt{x+7}</math> Se elevan al cuadrado los dos lados del igual

Otros tipos de ecuaciones (4ºESO Académicas)

De Wikipedia

Revisión de 21:49 1 ene 2009

Tabla de contenidos

Ecuaciones bicuadradas

Ecuaciones con la x en el denominador

Ecuaciones con radicales

Ecuaciones factorizadas: $(...) \cdot (...) \cdot (...) = 0$

Vistas

Herramientas personales

Menú

Buscar

Herramientas