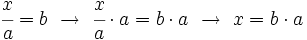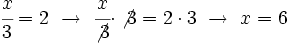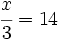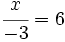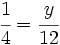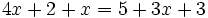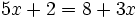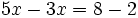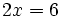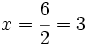Resolución de ecuaciones de primer grado (2º ESO)
De Wikipedia
| Revisión de 06:28 21 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:10 13 ene 2021 Coordinador (Discusión | contribuciones) (→Resolución de ecuaciones de primer grado en casos sencillos) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
| }} | }} | ||
| ==Resolución de ecuaciones de primer grado en casos sencillos== | ==Resolución de ecuaciones de primer grado en casos sencillos== | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=13'11" | ||
| + | |sinopsis=Una ecuación es una igualdad en la cual desconocemos uno de sus términos. Ese término que se desconoce se le llama incógnita y se suele escribir con una letra, que puede ser cualquier letra del abecedario, pero la que más se suele utilizar es la letra x, como en este caso. | ||
| + | |||
| + | Las ecuaciones tienen un grado. Según el grado que tengan se llaman ecuaciones de primer grado, de segundo, de tercero, etc. Para saber el grado de una ecuación, nos fijamos en la incógnita y el exponente mayor que haya nos indica el grado. | ||
| + | |||
| + | Resolver una ecuación es como jugar a ser detectives, porque es buscar qué valor tenemos que dar a la incógnita para que se cumpla esa igualdad. Así que tenemos que buscar mediante diferentes procedimientos cuál va a ser ese valor. | ||
| + | |||
| + | En este vídeo vamos a centrarnos en resolver ecuaciones de primer grado. Vamos a aprender el procedimiento que se sigue y comprenderemos de dónde viene. El procedimiento consiste en despejar la incógnita realizando lo que se llama trasposición de términos. | ||
| + | |||
| + | |||
| + | |url1=https://youtu.be/CN4n6Tfc5WI | ||
| + | }} | ||
| ===Resolución de ecuaciones de los tipos x+a=b=== | ===Resolución de ecuaciones de los tipos x+a=b=== | ||
| {{Resolucion de ecuaciones tipo I}} | {{Resolucion de ecuaciones tipo I}} | ||
Revisión de 19:10 13 ene 2021
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | 3º E.S.O. | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 139)
Introducción
Los siguientes videotutoriales condensan todo lo que vamos a ver en esta sección.
Lista de reproducción con 21 vídeos sobre ecuaciones de primer grado y problemas.
Resolución de ecuaciones de primer grado en casos sencillos
Una ecuación es una igualdad en la cual desconocemos uno de sus términos. Ese término que se desconoce se le llama incógnita y se suele escribir con una letra, que puede ser cualquier letra del abecedario, pero la que más se suele utilizar es la letra x, como en este caso.
Las ecuaciones tienen un grado. Según el grado que tengan se llaman ecuaciones de primer grado, de segundo, de tercero, etc. Para saber el grado de una ecuación, nos fijamos en la incógnita y el exponente mayor que haya nos indica el grado.
Resolver una ecuación es como jugar a ser detectives, porque es buscar qué valor tenemos que dar a la incógnita para que se cumpla esa igualdad. Así que tenemos que buscar mediante diferentes procedimientos cuál va a ser ese valor.
En este vídeo vamos a centrarnos en resolver ecuaciones de primer grado. Vamos a aprender el procedimiento que se sigue y comprenderemos de dónde viene. El procedimiento consiste en despejar la incógnita realizando lo que se llama trasposición de términos.
Resolución de ecuaciones de los tipos x+a=b
Procedimiento
Las ecuaciones del tipo 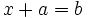 se resuelven restando
se resuelven restando  en ambos miembros:
en ambos miembros:
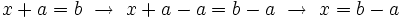
O lo que es lo mismo, si  está sumando en un miembro, lo podemos pasar restando al otro miembro, y la ecuación obtenida es equivalente.
está sumando en un miembro, lo podemos pasar restando al otro miembro, y la ecuación obtenida es equivalente.
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
(1ª parte de 2)
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
(2ª parte de 2)
Resuelve: 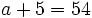
Resuelve: 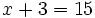
Resolución de ecuaciones del tipo x-a=b
Procedimiento
Las ecuaciones del tipo 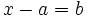 se resuelven sumando
se resuelven sumando  en ambos miembros:
en ambos miembros:
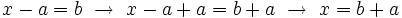
O lo que es lo mismo, si  está restando en un miembro, lo podemos pasar sumando al otro miembro, y la ecuación obtenida es equivalente.
está restando en un miembro, lo podemos pasar sumando al otro miembro, y la ecuación obtenida es equivalente.
Resolución de ecuaciones del tipo a·x=b
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
(1ª parte de 2)
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
(2ª parte de 2)
Resuelve: 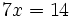
Resuelve: 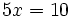
Resolución de ecuaciones del tipo x/a=b
Actividades y videotutoriales
Resuelve:
- a)
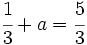
- b)
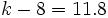
Resolución de ecuaciones en casos sencillos.
Resolución de ecuaciones en casos sencillos.
Resolución de ecuaciones en casos sencillos con fracciones.
Resolución de ecuaciones en casos sencillos.
Resolución de ecuaciones en casos sencillos.
Resolución de ecuaciones en casos sencillos con fracciones.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de ecuaciones sencillas |
(Pág. 140)
Resolución de ecuaciones de primer grado en casos más generales
Procedimiento
Para resolver ecuaciones de primer grado con una incógnita transformaremos la ecuación de partida en otra equivalente, más sencilla, por medio de los siguientes recursos:
- Reduciendo sus miembros, es decir, agrupando términos semejantes.
- Trasponiendo términos, esto es, utilizando las técnicas para casos sencillos vistas en los apartados anteriores.
Ejemplos de resolución de ecuaciones de primer grado sencillas y más generales.
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas o la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
Resolviendo ecuaciones de primer grado de forma intuitiva.
Una ecuación la podemos ver como una balanza en equilibrio. Si quitamos o ponemos las mismas pesas o la misma fracción de pesas de ambos lados de la balanza, la balanza sigue estando en equilibrio. Esta técnica me va a permitir resolver ecuaciones.
(Caso en el que hay variables en ambos lados)
Resolviendo ecuaciones de primer grado de forma intuitiva.
(Caso en el que hay variables en ambos lados)
Resuelve: 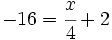
Resuelve: 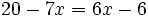
Resuelve: 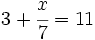
Resuelve: 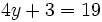
Resuelve: 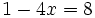
Resuelve: 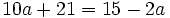
Resuelve: 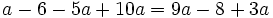
Resuelve: 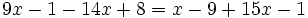
Resuelve: 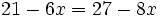
Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado.
Practica la resolución de ecuaciones de primer grado.
Ejemplos de resolución de ecuaciones de primer grado:
Pulsa el botón EJEMPLO para ver más ecuaciones.
Resolución de ecuaciones de primer grado.
Resolución de ecuaciones de primer grado guiada.
Resolución de ecuaciones de primer grado.
Resolución de ecuaciones de primer grado con variables en ambos lados.
Resolución de ecuaciones de primer grado con niveles de dificultad (empieza con nivel 4 pero puedes bajarlo hasta el 1).
Resolución de ecuaciones de primer grado con diversos grados de dificultad.
Resolución de ecuaciones con paréntesis o denominadores
Procedimiento
- En el caso de que la ecuación presente paréntesis, éstos se efectuarán en primer lugar.
- En el caso de que algunos de los términos de la ecuación tengan denominador, todos los términos de la ecuación se multiplicarán por el m.c.m. de dichos denominadores.
Ejemplos de resolución de ecuaciones de primer grado con paréntesis.
Ejemplos de resolución de ecuaciones de primer grado con denominadores.
Ejemplos de resolución de ecuaciones de primer grado con denominadores.
Ecuaciones con paréntesis:
Resuelve la ecuación: 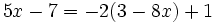
Resuelve la ecuación: 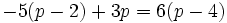
Resuelve la ecuación: 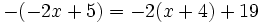
Resuelve:
a) 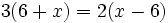
b) 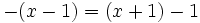
c) 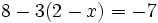
Resuelve:
a) 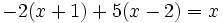
b) 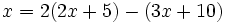
c) 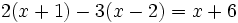
Resuelve: 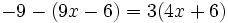
Ecuaciones con denominadores:
Resuelve:
a) 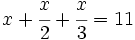
b) 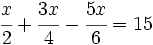
c) 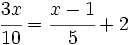
Resuelve: 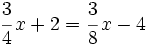
Ecuaciones con la variable en el denominador:
Resuelve: 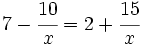
Resuelve: 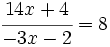
Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado con o sin paréntesis.
Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado con denominadores.
Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado con paréntesis y denominadores.
Practica la resolución de ecuaciones de primer grado con paréntesis y denominadores.
Ejercicios interactivos para practicar la resolución de ecuaciones de primer grado con paréntesis y denominadores (3 niveles).
Resolución de ecuaciones de primer grado con variables en ambos lados y con números racionales.
Resolución de ecuaciones de primer grado con paréntesis.
Resolución de ecuaciones de primer grado con paréntesis y números racionales.
Actividades y videotutoriales
Resuelve:
a) 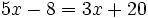
b) 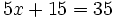
c) 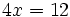
Resuelve:
a) 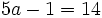
b) 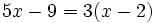
c) 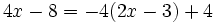
Resuelve:
a) 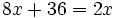
b) 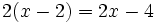
c) 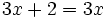
d) 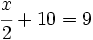
e) 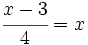
Resuelve:
a) 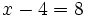
b) 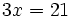
c) 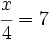
d) 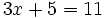
e) 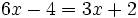
f) 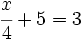
g) 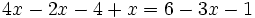
h) 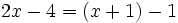
i) 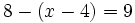
Repaso de resolución de ecuaciones de primer grado.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de ecuaciones más generales |
|
Ejercicios propuestos: Resolución de ecuaciones con denominadores |
Resolución de problemas mediante ecuaciones de primer grado
Procedimiento
Para resolver un problema mediante una ecuación hay que seguir los siguientes pasos:
- Determinar la incógnita.
- Traducir el enunciado del problema al lenguaje algebraico mediante una ecuación en la que intervenga la incógnita.
- Resolver la ecuación, es decir, hallar el valor de la incógnita.
- Dar la solución del problema a partir del valor obtenido de la incógnita.
Problemas resueltos: Resolución de problemas mediante ecuaciones
- Al sumar un número natural con el doble de sus siguiente, se obtiene 14. ¿Cuál es el número?
- El supermercado vende la bolsa de naranjas de cinco kilos al mismo precio que la caja de fresas de dos kilos. Así, el kilo de fresas sale a 1.80 € más caro que el de naranjas. ¿A cómo sale el kilo de naranjas y a cómo el de fresas?
- Para cercar una finca rectangular, 18 metros más larga que ancha, se han necesitado 24 rollos de alambrada de 10 metros cada uno. ¿Cuáles son las dimensiones de la finca?
- Luis tiene que hacer una serie de ejercicios durante el fin de semana. El sábado hace la mitad por la mañana y la tercera parte por la tarde, dejando el resto para el domingo. ¿Cuántos ejercicios tenía que hacer?
- Calcula las dimensiones de una finca rectangular, sabiendo que es 80 m más larga que ancha y que su perímetro es de 560 m.
- El número es el 4.
- Naranjas: 1.20 €/kg; fresas: 3 €/kg
- La finca mide 51 m x 69 m
- 24 ejercicios.
- Las dimensiones son: 100 m x 180 m.
- Pedro y yo hemos ganado jugando a la quiniela 69 €. Queremos repartirlo de modo que a Pedro le corresoponda el doble que a mi, puesto que ha invertido el doble al sellar la quiniela. ¿Cuánto le corresponde a cada uno?
- Si a un número le sumamos el triple del número anterior resulta 41. ¿Cuál es dicho número?
- Ayer corté el césped del jardín. Por la mañana corté la mitad del césped y por la tarde la tercera parte. ¿Cuál era la extensión total de césped si me quedan por cortar 12 m2?
- El salón de mi casa es de planta rectangular y mide 3 metros más de largo que de ancho. ¿Cuáles son las dimensiones del salón sabiendo que su perímetro es de 30 metros?
El perímetro de un rectángulo es 75.6 cm. Si la base y la altura se diferencian en 12.2 cm, ¿cuál es sus área?
Marcia ha abierto recientemente su nueva tienda de computadores. Ella gana 27$ por cada computadora que vende y sus gastos mensuales son de $10 000. ¿Cuál es el mínimo número de computadoras que necesita vender en un mes para tener ganancias?
El perímetro del jardín de Erwin mide 60 metros. Si el largo del jardín mide 2 veces su ancho, ¿Cuáles son las dimensiones del jardín?
Pedro tiene una huerta con cierto número de naranjos. El tuvo que cortar 5 árboles para controlar los insectos. cada uno de los árboles restantes produjo 210 naranjas. Si la cosecha total fue de 41 790 naranjas, ¿Cuánto árboles había inicialmente en la huerta de Pedro?
La suma de 4 enteros impares consecutivos es igual a 136. ¿Cuáles son esos números?
La suma de 3 enteros impares consecutivos es igual a 231. ¿Cuáles es el más grande de esos números?
Halla el valor de x en el siguiente dibujo.
Actividades en la que aprenderás y practicarás la resolución de problemas mediante ecuaciones de primer grado.
Actividades en la que aprenderás y practicarás la resolución de problemas mediante ecuaciones de primer grado.
Practica la resolución de problemas de distintos tipos mediante ecuaciones de primer grado. (Nivel 1)
Practica la resolución de problemas de distintos tipos mediante ecuaciones de primer grado. (Nivel 2)
Dos números consecutivos suman 99. Averigua el primero de dichos números.
Plantea ecuaciones a partir de enunciados.
Plantea y resuelve ecuaciones a partir de enunciados.
Plantea y resuelve ecuaciones sobre números enteros consecutivos.
Tanda de 10 problemas de ecuaciones de primer grado.
Ejercicios propuestos
|
Ejercicios propuestos: Resolución de problemas mediante ecuaciones de primer grado |
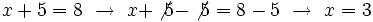
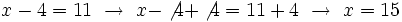
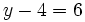
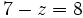
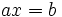 se resuelven dividiendo por
se resuelven dividiendo por 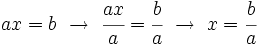
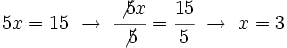
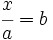 se resuelven multiplicando por
se resuelven multiplicando por