Aproximaciones

De Wikipedia

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Aproximaciones
- 1.1 Redondeo
- 1.2 Truncamiento
2 Errores
- 2.1 Error absoluto
- 2.2 Error relativo
3 Cota del error

[editar]

Aproximaciones

En la vida real suelen presentarse situaciones en las que no se puede, o no interesa realizar cálculos con valores exactos, bien porque éstos no se conocen, bien por que la información que ofrece el resultado exacto es irrelevante. En estas situaciones se recurre al cálculo con aproximaciones.

Así, cuando un número tiene muchas cifras, es difícil recordarlo y operar con él. Entonces, lo solemos sustituir por otro más manejable de valor similar, prescindiendo de sus últimas cifras. Por ejemplo, al escribir el número 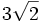$3\sqrt2$ queda reflejado con total precisión de qué número estamos hablando. Este número, tan sencillo de expresar con radicales, tiene, sin embargo, una expresión decimal que consta de infinitas cifras (4.2426406871192851464050661726291...). En la práctica, muchas veces es preferida la expresión decimal aproximada, con una cantidad reducida de cifras decimales (4.24), aunque ésta sea imprecisa, porque resulta más fácil captar su valor que expresándolo con radicales.

Otras veces, cuando hacemos una medición, el aparato de medida tiene limitaciones en cuanto a la precisión, por lo que la medida real no es posible averiguarla con exactitud y es sustituida por otra aproximada, más sencilla.

Una aproximación de un número es una representación inexacta de dicho número que, sin embargo, es suficientemente fiel como para ser útil.
Cuando aproximamos un número, nos quedamos con sus primeras cifras y completamos con ceros. Esas cifras, con las que nos quedamos, se llaman cifras significativas. A veces modificamos la última cifra con la que nos quedamos, dependiendo del tipo de aproximación que hagamos.
Llamamos orden de la aproximación, a la posición hasta la que nos quedamos con cifras significativas.
Se puede aproximar por defecto si el número utilizado es menor que el de partida, o por exceso si el número utilizado es mayor que el de partida.

Cifras significativas (12'17") Sinopsis:

Cifras significativas. Ejemplos.

Ejemplo: Aproximaciones

Aproxima por defecto y por exceso los siguientes números e indica el orden de la aproximación:

a) 263825 con 2 cifras significativas.

b) 6035192 con 1 cifra significativa.

c) 60.35 con 3 cifras significativas.

Solución:

   Número         Aproximación        Aproximación       Nº cifras          Orden de la
 de partida       por defecto          por exceso      significativas       aproximación
 ------------     ------------      --------------     --------------    -------------------
    263825    --->    260000   --->      270000    --->       2      ---> Decenas de millar
   6035192    --->   6000000   --->     7000000    --->       1      ---> Unidades de millón
        60.35 --->        60.3 --->          60.4  --->       3      ---> Décimas

[editar]

Redondeo

El redondeo es una forma de aproximar números. Para redondear un número a un determinado orden de unidades hay que:

Sustituir por ceros todas las cifras a la derecha de dicho orden.
Si la primera cifra sustituida es mayor o igual que cinco se suma una unidad a la cifra anterior.

Ejemplo: Redondeo

Redondea los siguientes números:

a) 27640.342 a la centena.

b) 3857.567 a la décima.

c) 24572.2578 a la unidad de millar.

Solución:

a) 27600 ; b) 3857.6 ; c) 25000

[editar]

Truncamiento

El truncamiento es una forma de aproximar números. Para truncar un número a un determinado orden de unidades se sustituyen por ceros todas las cifras a la derecha de dicho orden.

Ejemplo: Truncamiento

Trunca los siguientes números :

a) 27630.24578 a la milésima.

b) 3851.34 a la unidad.

c) 12345621.2 a la decena de millar.

Solución:

a) 27630.245 ; b) 3851 ; c) 12340000

Aproximaciones I Descripción:

Ejemplos de aproximaciones.
Ejercicios sobre redondeo.

Aproximaciones II Descripción:

Ejemplos de aproximaciones.
Ejercicios sobre truncamiento y redondeo.

Aproximaciones

Tutorial 1 (Redondeo y truncamiento) (7'37") Sinopsis:

Aproximaciones de números decimales por redondeo y truncamiento. Ejemplos.

Tutorial 2 (Redondeo y truncamiento) (4'28") Sinopsis:

Aproximaciones de números decimales por redondeo y truncamiento. Ejemplos.

Tutorial 3 (Aprox. por defecto y por exceso. Redondeo y truncamiento) (16'51") Sinopsis:

Aproximaciones de números decimales por defecto, por exceso, redondeo y truncamiento. Ejemplos.

Tutorial 4 (Redondeo) (8'32") Sinopsis:

Redondeo de números decimales. Ejemplos.

Redondeo y truncado de números decimales Descripción:

En esta escena podrás practicar a redondear y truncar números decimales.

[editar]

Errores

Cuando damos una cantidad de forma aproximada, cometemos un error. Distinguiremos los siguientes tipos de errores:

[editar]

Error absoluto

El error absoluto (E.A.) es la diferencia entre el valor real, V_r , y el aproximado, V_a , en valor absoluto, es decir, siempre con signo positivo.

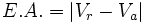
$E.A.= |V_r - V_a|\;$

Ejemplo: Error absoluto

Una montaña mide 2475 m. Redondea la altura a las centenas y halla el error absoluto cometido:

Solución:

a) Redondeando a las centenas, la montaña mide 2500 m.

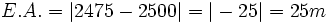
b) $E.A. = |2475 - 2500| = |-25| = 25 m\;$

[editar]

Error relativo

El error relativo (E.R.) es el cociente entre el error absoluto y el valor real.

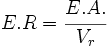
$E. R= \cfrac {E.A.}{V_r}$

Ejemplo: Error relativo

Una montaña mide 2475 m. Redondea la altura a las centenas y halla el error relativo cometido:

Solución:

a) Redondeando a las centenas, la montaña mide 2500 m.

b) 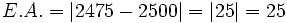$E.A. = |2475 - 2500| = |25| = 25 \;$

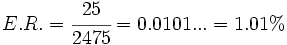
c) $E.R. = \cfrac {25}{2475}=0.0101...=1.01%$

Error absoluto y relativo

Tutorial (11'21") Sinopsis:

Tutorial que explica los errores en aproximaciones (absoluto y relativo) así como la información aportada por estos valores.

Ejemplo (2'35") Sinopsis:

Ejemplo práctico sobre el cálculo del error absoluto y el error relativo.

Ejemplos: Aproximaciones de fracciones y los errores cometidos

En la siguiente escena se muestran ejemplos de como se redondea ó trunca una fracción a un orden determinado de decimales, así como los errores absoluto y relativo cometidos.

Pulsa "Inicio" para obtener un nuevo ejemplo.

Introduce el orden de la aproximación en la casilla correspondiente y pulsa "Redondeo" o "Truncamiento" para obtener distintos tipos de aproximaciones.

Anota algún ejemplo en tu cuaderno.

Medida de errores I Descripción:

Error absoluto, error relativo y cota del error. Ejemplos.
Ejercicios sobre errores y cotas.

Medida de errores II Descripción:

Error absoluto, error relativo y cota del error. Ejemplos.
Ejercicios sobre errores y cotas.

Ejercicios: Aproximaciones de fracciones y los errores cometidos Descripción:

Pulsa el botón "Ayuda" y lee atentamente la explicación del ejercicio.

[editar]

Cota del error

Para que la cantidad aproximada que utilizamos sea fiable, el error cometido debe estar controlado o acotado. Las cotas de error nos darán el máximo error que cometeremos al dar una aproximación de un número.

Llamaremos cota del error absoluto a un número k que cumpla que E.A. < k.
Llamaremos cota del error relativo a un número k´ que cumpla que E.R. < k´.

Cotas del error absoluto y relativo

Cuando redondeamos un valor, podemos dar cotas de los errores de la siguiente manera:

Cota de error absoluto: k = 5 unidades del orden de la primera cifra no utilizada en el redondeo.
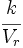
Cota del error relativo: k´ = $\cfrac{k} {V_r}$

Cuando el valor real no es conocido (sólo tenemos un valor aproximado), el cálculo de las cotas del error se hace de la siguiente manera:

Cota de error absoluto: k = 5 unidades del orden de la primera cifra no significativa.
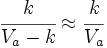
Cota del error relativo: k´ = $\cfrac{k} {V_a - k} \approx \cfrac{k} {V_a}$

Ejemplo: Cota del error

a) Una montaña mide 2475 m. Halla la cota de los errores absoluto y relativo cometidos en el redondeo a las centenas.

b) Una montaña (que no se sabe lo que mide realmente) mide, aproximadamente, 2500 m (esta sería la cantidad redondeada). Halla la cota de los errores absoluto y relativo.

Solución:

Redondeando a las centenas, la montaña mide 2500 m. a) Al redondear la primera cifra no utilizada es la de las decenas. De esta forma, la cotas de error son:

Cota de error absoluto: k = 50
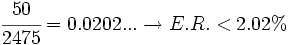
Cota del error relativo: k´ = $\cfrac{50}{2475} = 0.0202... \rightarrow E.R.< 2.02%$

b) Como la cantidad redondeada es 2500 m, la primera cifra no significativa es la de las decenas. De esta forma, la cotas de error son:

Cota de error absoluto: k = 50
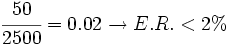
Cota del error relativo: k´ = $\cfrac{50}{2500} = 0.02 \rightarrow E.R.< 2%$

Corolario

Cuantas más cifras significativas se utilicen para dar una medida aproximada, menor es el error relativo cometido.

Ejercicio resuelto 1: Cota del error

Qué podemos decir del error absoluto y del error relativo de las siguientes mediciones:

a) La altura de un edificio es de 92 m.

b) La altura a la que vuela un avión es de 9.2 km.

c) La altura a la que está un satélite artificial es de 920 km.

Solución:

Cota error absoluto: k = 5 unidades del orden de la primera cifra no significativa

a) k = 0.5 m.

b) k = 0.05 km = 50 m.

c) k = 5 km = 5000 m.

Son muy distintos.

Cota error relativo: k´ = 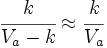$\cfrac{k} {V_a - k} \approx \cfrac{k} {V_a}$

a) k' = 0.5 m : 92 m = 0.00543...

b) k' = 0.05 km : 9.2 km = 0.00543...

c) k' = 5 km : 920 km = 0.00543...

Son iguales.

Conclusión: Aunque haya diferencia en el error absoluto, las mediciones tienen igual precisión.

Ejercicio resuelto 2: Cota del error

Comparar el error relativo cometido en estas mediciones:

a) 87 m b) 5 km c) 453 km d) 4.53·10¹¹ km

Solución:

El mayor error relativo se da en el apartado b), ya que sólo tiene una cifra significativa.

El menor error relativo se puede dar en el apartado c) o d), por tener tres cifras significativas. Ambos tienen el mismo error realtivo por ser las tres cifras significativas iguales.

a) k' = 0.5 m : 87 m = 0,0057...

b) k' = 0.5 km : 5 km = 0.1

c) k' = 0.5 km : 453 km = 0,0011...

d) k' = 0.005·10¹¹ km : 4.53·10¹¹ km = 0,0011...

Cota del error (9') Sinopsis:

Videotutorial sobre las cotas de error absoluto y relativo.

Obtenido de "http://maralboran.org/wikipedia/index.php/Aproximaciones"

Categorías: Matemáticas | Números

Aproximaciones

De Wikipedia

Tabla de contenidos

Aproximaciones

Redondeo

Truncamiento

Errores

Error absoluto

Error relativo

Cota del error

Vistas

Herramientas personales

Menú

Buscar

Herramientas