Cantor
De Wikipedia
Georg Ferdinand Ludwig Philipp Cantor (1845 – 1918), matemático alemán, nacido en Rusia. Es principalmente conocido por su teoría de conjuntos, que se ha convertido en una teoría fundamental de las matemáticas. Cantor estableció la importancia de las correspondencias biunívocas entre conjuntos, definió los conjuntos infinitos y los conjuntos bien ordenados, y probó que los números reales son "más numerososo" que los números naturales. De hecho, el teorema de Cantor, implica la existencia de una "infinidad de infinitos". Definió los números cardinales y ordinales y su aritmética. El trabajo de cantor es de gran interés filosófico.
La teoría de Cantor de los números transfinitos fue considerada originalmente tan anti-intuitiva, e incluso chocante, que encontró resistencia por parte de los matemáticos contemporáneos como Leopold Kronecker y Henri Poincaré y, posteriormente, de Hermann Weyl y LEJ Brouwer, mientras que Ludwig Wittgenstein planteó objeciones filosóficas. Algunos teólogos cristianos (en particular neo-escolásticos) vieron el trabajo de Cantor como un desafío a la unicidad del infinito absoluto en la naturaleza de Dios, equiparando, en una ocasión,la teoría de números transfinitos con el panteísmo. Las objeciones a su trabajo a veces fueron feroz: Poincaré se refiere a las ideas de Cantor como una "grave enfermedad" que infecta la disciplina de las matemáticas, y la oposición pública y los ataques personales de Kronecker ponían a Cantor como un "científico charlatán", un "renegado" y un "corruptor de la juventud.
"Décadas después de la muerte de Cantor, Wittgenstein, en sus escritos, lamentó que la matemática hubiese "cabalgado y cabalgado con los perniciosos modismos de teoría de conjuntos", que desestimó como "totalmente absurda, ridícula y erronea".
Los recurrentes episodios de depresión de cantor desde 1884 hasta el final de su vida pudieron deberse a la actitud hostil de muchos de sus contemporáneos, pero estos episodios también pueden ser vistos como probables manifestaciones de un trastorno bipolar.
Las duras críticas han sido acompañadas de elogios internacionales. En 1904, la Royal Society concedió a Cantor la Medalla Sylvester, el más alto honor que puede conferir. Como anécdotas, mencionar que Cantor creía que su teoría de los números transfinita le había sido comunicada por Dios. Y es famosa la defensa que hace David Hilbert de sus críticos: "Nadie nos podrá expulsar del paraíso que Cantor ha creado."
Tabla de contenidos |
Vida
Juventud y estudios
Cantor nació en 1845 en la colonia de comerciantres occidental en San Petersburgo, Rusia, y criado en la ciudad hasta que tuvo once años. Era el mayor de seis hijos y fue un destacado violinista, habiendo heredado de sus padres considerables talentos artísticos y musicales. Su padre padre había sido miembro de la Bolsa de San Petersburgo; cuando enfermó, la familia se mudó a Alemania en 1856, primero a Wiesbaden y luego a Frankfurt, buscando inviernos más suaves que los de San Petersburgo. En 1860, Cantor se graduó con méritos en la Realschule de Darmstadt; sus excepcionales habilidades en matemáticas, en particular en trigonometría, fueron notorias. En 1862, Cantor ingresó en el Instituto Politécnico Federal de Zürich, hoy el ETH (Instituto Federal Suizo de tecnología) de Zurich. Tras recibir una importante herencia a la muerte de su padre en 1863, Cantor trasladó sus estudios a la Universidad de Berlín, donde asistió a conferencias de Leopold Kronecker, Karl Weierstrass y Ernst Kummer. Pasó el verano de 1866 en la Universidad de Göttingen que, por aquel entonces y posteriormente, fue un importante centro de investigación matemática.
Profesor e investigador
Después de enseñar brevemente en una escuela para niñas de Berlín, Cantor ocupó una plaza en la Universidad de Halle, donde pasó toda su carrera. En 1867, le otorgaron el doctorado por una tesis sobre la teoría de los números, De aequationibus secundi gradus indeterminatis. En 1874, Cantor se casó con Vally Guttmann. Tuvieron seis hijos, el último nacido en 1886. Cantor fue capaz de mantener una familia, a pesar de su modesta paga académica, gracias a la herencia de su padre. Durante su luna de miel en el Harz, Cantor pasó mucho tiempo de discusiones matemáticas con Richard Dedekind, con quien entabló amistad dos años antes, mientras pasaba unas vacaciones en Suiza.
Cantor fue ascendido a Profesor extraordinario en 1872, y profesor titular en 1879. Alcanzar este último rango a la edad de 34 fue un logro notable, pero Cantor deseaba una plaza en una universidad de mayor prestigio, en particular, en Berlín, por entonces la principal universidad alemana. Sin embargo, su trabajo encontró demasiada oposición para que esto fuera posible. Kronecker, quien encabezó las matemáticas en Berlín hasta su muerte en 1891, se sentía cada vez más incómodo con la perspectiva de tener a Cantor como un compañero de trabajo, y lo veía como un "corruptor de la juventud" por enseñar sus ideas a una joven generación de matemáticos. Peor aún, Kronecker, una figura bien establecida dentro de la comunidad matemática y ex-profesor de Cantor, estaba en desacuerdo con la orientación de la labor de Cantor. Kronecker, ahora visto como uno de los fundadores de la matemática desde un punto de vista constructivo, no gustaba mucho de la teoría de conjuntos de Cantor, ya que afirmaba la existencia de conjuntos que cumplen ciertas propiedades, sin dar ejemplos específicos de conjuntos, cuyos elementos cumpliesen esas propiedades. Cantor llegó a creer que la postura de Kronecker le haría imposible dejar nunca Halle.
En 1881, Eduard Heine, un colega Cantor en Halle, murió, dejando una plaza vacante. Halle aceptó la sugerencia de Cantor de que se le ofreciese a Dedekind, M. Heinrich Weber y Franz Mertens, en ese orden, pero todos la rechazaron tras habersela ofrecido. Fue nombrado Friedrich Wangerin, pero éste nunca estuvo cerca de Cantor.
En 1882 la correspondencia matemática entre Cantor y Dedekind llegó a su fin, al parecer como resultado de la negativa de Dedekind de aceptar la plaza en Halle. Cantor comenzó también otra importante correspondencia con Gösta Mittag-Leffler en Suecia, y pronto comenzó a publicar en la revista de Mittag-Leffler, Acta Mathematica. Pero en 1885, Mittag-Leffler estaba preocupado por la naturaleza filosófica y la nueva terminología de un documento enviado por Cantor a la revista. Pidió Cantor que retirase el documento de Acta, mientras lo tenían a prueba, durante un periodo de al menos 100 años. Cantor cumplió, pero se dirigió por escrito a un tercero: " Mittag-Leffler tiene su forma de actuar, y tendría que esperar hasta el año 1984, lo cual me parece una demanda excesiva! ... Pero, por supuesto, No quiero saber nada más de Acta Mathematica."
Cantor entonces redució drásticamente su relación y correspondencia con Mittag-Leffler, mostrando una tendencia a interpretar las críticas bien intencionadas como una profunda afrenta personal.
Cantor sufrió su primer brote conocido de depresión en 1884. La crítica de su trabajo pesaba sobre su mente: cada una de las cincuenta y dos cartas que escribió a Mittag-Leffler en 1884, atacaban a Kronecker. Un pasaje de una de estas cartas es revelador de los daños a la autoconfianza de Cantor: " ... no sé cuándo voy a volver a continuar con mi trabajo científico. Por el momento no puedo hacer absolutamente nada, y limitarme al más necesario deber de mis conferencias; cuánto más feliz sería estando científicamente activo, si sólo tuviera la frescura mental necesaria. "
Esta crisis emocional lo llevó a dar clases de filosofía en lugar de matemáticas. También se inició un intenso estudio de la literatura isabelina, en un intento de demostrar que Francis Bacon escribió las obras atribuidas a Shakespeare, que culminaron en dos folletos, publicados en 1896 y 1897.
Cantor se recuperó poco después e hizo otras contribuciones importantes, incluyendo su famoso teoerma, el teorema de Cantor, y su argumento de la diagonal. Sin embargo, nunca más alcanzó el alto nivel de sus notables trabajos del periodo de 1874 a 1884. Finalmente buscó una reconciliación con Kronecker, que Kronecker tuvo la amabilidad de aceptar. Sin embargo, los desacuerdos y las dificultades filosóficas siguieron dividiéndolos. Antes se pensaba que los recurrentes episodios de depresión de cantor fueron provocados por la oposición de Kronecker a su trabajo. Si bien las preocupaciones matemáticas de Cantor y sus dificultades para hacer frente a ciertas personas se vieron muy magnificadas por su depresión, es dudoso que esta fuera la causa. Por el contrario, su diagnóstico póstumo de bipolaridad ha sido aceptado como la causa de su irregular estado de ánimo.
En 1890, Cantor jugó un papel decisivo en la fundación de la Deutsche Mathematiker-Vereinigung y presidido su primera reunión en Halle en 1891. Su reputación era lo suficientemente fuerte, a pesar de la oposición de Kronecker a su trabajo, como para garantizar su elección como primer presidente de esta sociedad. Dejando a un lado la animosidad que sentía hacia Kronecker, Cantor le invitó a dirigir la reunión. pero Kronecker no pudo hacerlo porque su esposa se estaba muriendo.
Últimos días
Después de ser hospitalizado en 1884, no hay constancia de que Cantor hubiese estado en ningún otro sanatorio hasta 1899. Poco después de la segunda hospitalización, su hijo menor murió de repente (mientras Cantor daba una conferencia sobre sus puntos de vista sobre la teoría de Bacon y William Shakespeare) , y esta tragedia drenó gran parte de su pasión por las matemáticas. Cantor fue hospitalizado de nuevo en 1903. Un año más tarde, se indignó y agitó por un documento presentado por Julius König en el Tercer Congreso Internacional de Matemáticos. En el documento intentó demostrar que los principios básicos de la teoría de conjuntos transfinita eran falsos. Dado que había sido leído delante de sus hijas y sus colegas, Cantor lo percibió como una humillación pública. Aunque Ernst Zermelo demostró menos de un día después que la demostración de König estaba mal, Cantor siguió afectado, llegando incluso a cuestionar a Dios. Cantor sufrió de depresión crónica el resto de su vida, por lo que fue dispensado de la enseñanza en varias ocasiones y varias veces confinado en diversos sanatorios. Los acontecimientos de 1904 precedieron una serie de hospitalizaciones, a intervalos de dos o tres años. Sin embargo, él no abandonó por completo las matemáticas, dando una conferencia sobre las paradojas de la teoría de conjuntos (paradoja de Burali-Forti, la paradoja de Cantor, y la paradoja de Russell) en una reunión de la Deutsche Mathematiker-Vereinigung en 1903, y asistiendo al Congreso Internacional de Matemáticos en Heidelberg en 1904.
En 1911, Cantor fue uno de los distinguidos académicos extranjeros invitados a asistir al 500º aniversario de la fundación de la Universidad de St. Andrews en Escocia. Cantor asistió, con la esperanza de encontrarse con Bertrand Russell, cuyo recién publicado Principia Mathematica citaba, repetidas veces, el trabajo de Cantor del trabajo, pero esto no llegó a suceder. Al año siguiente, St Andrews concedió a Cantor el título de Doctor Honoris Causa, pero su enfermedad le impidió recibirlo en persona.
Cantor se retiró en 1913, y padeció pobreza y malnutrición durante la Primera Guerra Mundial. La celebración pública de su 70 cumpleaños fue cancelada a causa de la guerra. Murió el 6 de enero de 1918 en el sanatorio donde había pasado el último año de su vida.
Matemáticas
El trabajo de Cantor entre 1874 y 1884 da origen a la teoría de conjuntos. Antes de este trabajo, el concepto de conjunto era más bien elemental habiéndose utilizado implícitamente desde los inicios de la matemática, remontandose a las ideas de Aristóteles. Nadie había caido en la cuenta de que la teoría de conjuntos carecía de contenido no trivial: Antes de Cantor sólo había conjuntos finitos (que eran fáciles de entender) y "el infinito" (que era considerado más un tema de debate filosófico que matemático). Demostrando que había infinitos posibles tamaños de conjuntos infinitos, Cantor estableció que la teoría de conjuntos no era trivial, y que necesitaba ser estudiada. La teoría de conjuntos ha llegado a desempeñar el papel de una teoría fundamental en la matemática moderna, en el sentido de que interpreta proposiciones acerca de objetos matemáticos (por ejemplo, los números y funciones) de todas las áreas tradicionales de las matemáticas (como álgebra, análisis y topología) en una sola teoría, y proporciona un conjunto de axiomas para demostrarlas o refutarlas. Los conceptos básicos de las teoría de conjuntos son utilizados actualmente en matemáticas.
En uno de sus primeros escritos, Cantor demostró que el conjunto de los números reales es "más numeroso" que el conjunto de números naturales, lo que puso de manifiesto, por primera vez, que existen infinidad de conjuntos de diferentes tamaños. También fue el primero en reconocer la importancia de las correspondencias biyectivas( o correspondencias "1-a-1") en la teoría de conjuntos. Utilizó este concepto para definir los conjuntos finitos y los conjuntos infinitos, clasificando estos últimos en numerables y no numerables.
Cantor introdujo construcciones fundamentales en teoría de conjuntos, tales como el conjunto potencia de un conjunto A, que es el conjunto de todos los subconjuntos de A. Más tarde, demostró que el tamaño de la potencia de un conjunto es estrictamente más grande que el tamaño de A, incluso cuando A es un conjunto infinito; este resultado pronto fue conocido como el teorema de Cantor. Cantor desarrolló toda una teoría y una aritmética de los conjuntos infinitos, llamados cardinales y ordinales, que extendió la aritmética de los números naturales. Su notación para los números cardinales es la letra hebrea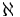 
(Aleph), con un subíndice natural; para los ordinales usó la letra griega ω (omega). Esta notación está en uso hoy en día.
La hipótesis del continuo introducida por Cantor, fue presentada por David Hilbert como el primero de sus veintitrés problemas abiertos en su famoso discurso del año 1900 en el Congreso Internacional de Matemáticos de París. Los elogios de Hilbert atrajeron fama al trabajo de Cantor. El filósofo estadounidense, Charles Peirce, elogió la teoría de conjuntos de Cantor, y, a raíz de conferencias públicas de Cantor en el primer Congreso Internacional de Matemáticos, celebrado en Zurich en 1897, Hurwitz y Hadamard, también expresaron su admiración. En ese Congreso, Cantor renovó su amistad y su correspondencia con Dedekind. Desde 1905, Cantor se correspondía con su, a la par, admirador y traductor, el británico Philip Jourdain, sobre la historia de la teoría de conjuntos de Cantor y sus ideas religiosas. Esto fue publicado posteriormente, así como varias de sus obras de exposición.
Teoría de números y teoría de funciones
Los diez primeros documentos de cantor eran sobre la teoría de números, su tema de tesis. A propuesta de Eduard Heine, el profesor de Halle, Cantor se centró en el análisis. Heine le propuso resolver un problema abierto que habían eludido Dirichlet, Lipschitz, Bernhard Riemann, y el propio Heine: la unicidad de la representación de una función mediante series trigonométricas. Cantor resolvió este difícil problema en 1869. Entre 1870 y 1872, Cantor publicó más documentos sobre series trigonométricas, incluyendo una definición de los números irracionales como sucesiones convergentes de números racionales. Dedekind, con quien Cantor entabló amistad en 1872, citó este documento más tarde, ese mismo año, en un documento donde estableció por primera vez su célebre definición de números reales mediante cortaduras de Dedekind.
Teoría de conjuntos
Correspondencias biyectivas
Hipótesis del continuo
Cantor fue el primero en formular lo que más tarde llegó a ser conocida como la hipótesis del continuo: no existe ningún conjunto cuya potencia es mayor que el de los naturales y menor que el de los reales (o equivalentemente, la cardinalidad de los reales es exactamente Aleph-uno). Cantor creía que la hipótesis del continuo era cierta e intentó probarla, en vano, durante muchos años, lo que le causó una gran ansiedad.
La dificultad que Cantor tuvo par demostrar la hipótesis del continuo ha sido subrayada por posteriores desarrollos en el campo de las matemáticas: Un resultado de 1940 por Gödel y otro de 1963 por Paul Cohen, juntos implican que la hipótesis del continuo no puede ser probada ni refutada utilizando la teoría de conjuntos de Zermelo-Fraenkel más el axioma de elección.
Paradojas de la teoría de conjuntos
Los debates sobre las paradojas de la teoría de conjuntos comenzaron a aparecer a finales del siglo XIX. Algunas de estas implicaron problemas fundamentales en la teoría de conjuntos de Cantor. En 1897 Cesare Burali Forti estableció la primera de esas paradojaa, la paradoja de Burali Forti: el número ordinal del conjunto de todos los ordinales debe ser un ordinal y esto conduce a una contradicción. Cantor descubrió esta paradoja en 1895, y la describió en 1896 una carta a Hilbert. las críticas que se levantaron llevaron a Cantor a lanzar contra-argumentos en 1903, destinados a defender los principios básicos de su teoría de conjuntos.
En 1899, Cantor descubrió su homónima paradoja, la paradoja de Cantor: ¿cuál es el número cardinal del conjunto de todos los conjuntos? Es evidente que debe ser el mayor de todos los posibles cardinales. Sin embargo, para cualquier conjunto A, el número cardinal del conjunto potencia de ese conjunto es estrictamente mayor que el número cardinal de A (este hecho ahora se conoce como el teorema de Cantor).
Esta paradoja, junto con la de Burali Forti, llevó a Cantor a formular un concepto llamado la "limitación de tamaño", según el cual la recopilación de todos los ordinales, o de todos los conjuntos, era una "multiplicidad incompatible" que era "demasiado grande" para ser un conjunto. Estas colecciones se conocerían más tarde conocido como clases propias.
Una opinión común entre los matemáticos es que estas paradojas, junto con la paradoja de Russell, demuestran que no es posible hacer un enfoque "ingenuo", o no axiomático, de teoría de conjuntos sin correr el riesgo de contradicción, y es cierto que se encuentran entre las motivaciones de Zermelo y otros para axiomatizar la teoría de conjuntos.
