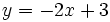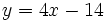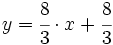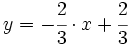Ecuaciones de la recta (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 167)
Ecuación explícita de una recta
La ecuación explícita de la recta viene dada por la ya conocida expresión:
|
|
 es la pendiente.
es la pendiente.
 es la ordenada en el origen.
es la ordenada en el origen.
En este video llama "ecuación en forma pendiente-ordenada en el origen" a lo que nosotros llamaremos "ecuación en forma explícita".
Representa: 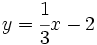
Una recta tiene pendiente -3/4 y pasa por el punto (0,8). Halla su ecuación explícita.
Introducción a la "forma explícita" o "forma pendiente-ordenada al origen" de la ecuación de la recta.
Ecuación de la recta en "forma explícita" o "forma pendiente-ordenada al origen". Representación gráfica.
Representación gráfica de rectas en forma explícita.
Introducción a la "forma explícita" o "forma pendiente-ordenada al origen" de la ecuación de la recta.
Representación gráfica de rectas en forma explícita.
Ecuación general o implícita de una recta
La ecuación de la recta también la podemos expresar con todos los términos en lado izquierdo de la ecuación, igualados a cero. Es lo que se denomina:Ecuación general o implícita de la recta:
|
|
Algunos autores llaman "forma general" de la ecuación de la recta a la que viene dada en la forma 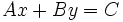
Ejemplo: Ecuación general
Halla la ecuación general de la recta 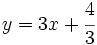 .
.
Nos dan la ecuación explícita:
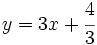
Tenemos que pasar todos los términos de la ecuación al lado izquierdo y ordenarlos:
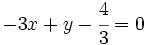
Opcionalmente, podemos quitar denominadores:
|
|
Proposición
Si una recta tiene como ecuación general 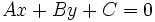 , entonces su pendiente es igual a:
, entonces su pendiente es igual a:
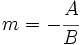
Demostración:
Partiremos de la ecuación general:
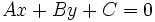
y despejaremos la variable  para obtener la ecuación explícita:
para obtener la ecuación explícita:
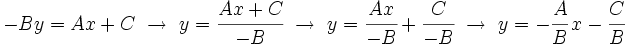
Como en la ecuación explícita, el coeficiente de la  es la pendiente, se tiene:
es la pendiente, se tiene:
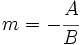
Dada la ecuación de la recta 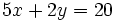 (para algunos autores esta es la "forma general"), obtén la ecuación explícita y represéntala gráficamente.
(para algunos autores esta es la "forma general"), obtén la ecuación explícita y represéntala gráficamente.
Dada la ecuación de la recta 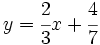 , obtén la ecuación general.
, obtén la ecuación general.
Actividades en las que aprenderás obtener la ecuación general de una recta y a representarla gráficamente.
Forma general de la ecuación de la recta.
Nota: En esta actividad la llaman "forma estándar" y usan el formato Ax+By=C.
Representa gráficamente a partir de la ecuación dada en forma general.
Nota: En esta actividad la llaman "forma estándar" y usan el formato Ax+By=C.
Expresa en forma general las ecuaciones de las rectas dadas.
Nota: En esta actividad la llaman "forma estándar" y usan el formato Ax+By=C.
Ecuación punto-pendiente de una recta
Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado:
Ecuación punto-pendiente
Sea 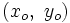 un punto de una recta y
un punto de una recta y  su pendiente, entonces su ecuación viene dada por:
su pendiente, entonces su ecuación viene dada por:
|
|
expresión que se denomina ecuación punto-pendiente de la recta.
Para comprobar que esta es la ecuación de la recta, comprobaremos que su pendiente es  y que pasa por el punto dado
y que pasa por el punto dado 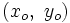 .
En efecto:
.
En efecto:
- Si desarrollamos la expresión de la ecuación punto-pendiente, se obtiene:
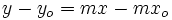
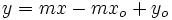
de donde se observa que el coeficiente e la x es  , y por tanto, la pendiente de la recta.
, y por tanto, la pendiente de la recta.
- Si sustituimos el punto
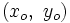 en la ecuación punto-pendiente, es decir, hacemos
en la ecuación punto-pendiente, es decir, hacemos 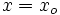 e
e 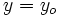 , se obtiene
, se obtiene
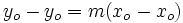
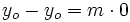
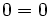
Ejemplo: Ecuación punto-pendiente
Halla la ecuación punto-pendiente de la recta que pasa por el punto (-2, 4) y tiene pendiente 3.
En la ecuación punto-pendiente:
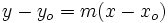
sustituimos 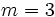 ,
, 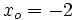 ,
, 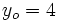 , obteniendo:
, obteniendo:
|
|
Introducción a la forma punto-pendiente de la ecuación de la recta.
Determina la ecuación general de la recta que pasa por el punto (-2,3) y es paralela a la recta 2x-3y=0.
Halla la ecuación de la recta que pasa por el origen de coordenadas y es paralela a al recta de ecuación 2x-y+3=0.
Actividades en las que aprenderás obtener la ecuación punto-pendiente de una recta.
En esta escena podrás practicar el cálculo de la ecuación de la recta con una cierta pendiente y que pasa por un punto dado.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuación punto-pendiente de la recta |
(Pág. 168)
Ecuación de la recta que pasa por dos puntos
Dos puntos determinan una única recta que pasa por ellos. Veamos como se obtiene su ecuación:
Procedimiento
Sean 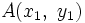 y
y 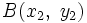 dos puntos de una recta, tales que
dos puntos de una recta, tales que 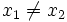 . Para hallar su ecuación procederemos como sigue:
. Para hallar su ecuación procederemos como sigue:
- Con los dos punto hallaremos la pendiente:
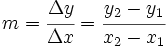
- A continuación podemos seguir dos caminos:
- a) Usar la ecuación punto-pendiente: con uno cualquiera de los dos puntos y con la pendiente que acabamos de calcular.
- b) Usar la ecuación explícita,
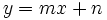 : sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de
: sustituyendo las coordenadas de uno de los dos puntos y el valor de la pendiente, despejaremos el valor de  .
.
Si 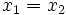 el procedimiento anterior no se puede aplicar, puesto que al hallar la pendiente en el primer paso el denominador se anula. En este caso decimos que la pendiente está indefinida. La recta resultante es una recta vertical y su ecuación es
el procedimiento anterior no se puede aplicar, puesto que al hallar la pendiente en el primer paso el denominador se anula. En este caso decimos que la pendiente está indefinida. La recta resultante es una recta vertical y su ecuación es 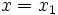 .
.
Determina la ecuación general de la recta que pasa por los puntos (2,1) y (3,-2).
Determina la ecuación general de la recta que pasa por los puntos (1,-2) y (3,4).
Determina la ecuación general de la recta que pasa por los puntos (3,2) y (-1,-2).
Si una recta pasa por los puntos (-2,-6) y (-5,p), y tiene pendiente -9/4, hallar el valor de "p".
Determina la ecuación explícita de la recta que tiene abscisa al origen 3 y ordenada al origen 5.
Halla la ecuación explícita de la recta que pasa por los puntos (-1,6) y (5,-4).
Halla la ecuación punto-pendiente y explícita de la recta que pasa por los puntos (4,9) y (6,1).
El número de calorias que se queman en una cinta de correr es una función de la velocidad de la cinta. Una persona que se ejercita a 2.5 millas por hora quemará 210 cal en una hora. A 6 millas por hora esta persona quemará 370 cal en una hora. Sea C las calorias quemadas en una hora y V la velocidad de la cinta, determina:
- a) Una función lineal C(V) que se ajuste a los datos.
- b) ¿Cuántas calorias se queman en una hora si la persona se ejercita a una velocidad de 5 millas por hora?
Actividades en las que aprenderás obtener la ecuación de la recta que pasa por dos puntos.
En esta escena podrás ver practicar el cálculo de la ecuación de la recta que pasa por dos puntos dados.
Halla la ecuación explícita de la recta que pasa por dos puntos.
Halla la ecuación punto-pendiente de la recta que pasa por dos puntos.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuación de la recta que pasa por dos puntos |
Ejercicios
Autoevaluación.
Problemas resueltos con funciones afines o de proporcionalidad directa:
- Obtener la función a partir de valores de la misma.
- Obtener la función a partir la pendiente y la ordenada en el origen de la misma.
Repaso de la forma punto-pendiente de la ecuación de la recta.
|
Ejercicios resueltos: Ecuaciones de la recta 1. Halla la ecuación de las siguientes rectas:
Solución:
2. Averigua si los puntos (0,3), (3,1) y (9,-4) están alineados. Solución: Se halla la ecuación de la recta que pasa por los dos primeros puntos y se comprueba que el tercer punto no verifica la ecuación. Por tanto no están alineados. |
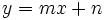
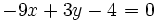
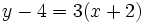
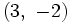 .
.
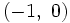 y
y 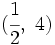 .
.
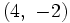 y es paralela a la recta
y es paralela a la recta 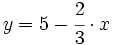 .
.